Combination Sum II – Find all unique combinations

We shall answer the most often requested interview question “Combination Sum II – Find all unique combinations” in this post.

Find all unique combinations in candidates where the candidate numbers add to target given a set of candidate numbers (candidates) and a target number. Every number in the candidates could just be used once in the mix.

Note: The set of solutions has to be devoid of repeating combinations.

Some instances are:

Example 1:

Input: candidates = [10,1,2,7,6,1,5], target = 8

Output: 
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]]


Explanation: These are the unique combinations whose sum is equal to target.
 
Example 2:

Input: candidates = [2,5,2,1,2], target = 5

Output: [[1,2,2],[5]]

Explanation: These are the unique combinations whose sum is equal to target.

Solution:

Disclaimer: Don’t jump directly to the solution, try it out yourself first.

Solution 1: Using extra space and time complexity 

Approach:

Defining the Recursive Function:

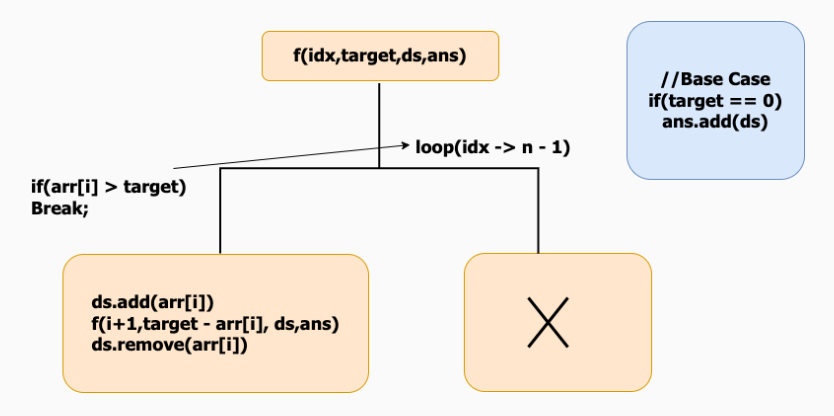
Sort the elements before beginning the recursive call; the ans should not be duplicated and should include the combinations in sorted sequence.

We begin with the index 0; at index 0 we have n – 1 ways to choose the first element of our subsequence.

See if our ds could benefit from the current index value. If so, include it into the ds and shift the index by one. As shifting the index skip the consecutive repeated elements will create duplicate sequences.

After the call make sure to pop the element from the ds. Reduce the target by arr[i] and call the recursive call for f(idx + 1,target – 1,ds,ans).(Seeing the example repeatedly will help you to grasp).

If arr[i] > target, then stop the recursive function since there is no need in checking; the index will be moving by 1 all the entries to its right will be in increasing order.

Base state:

Add the ds to the ans return anyhow the goal value is zero.

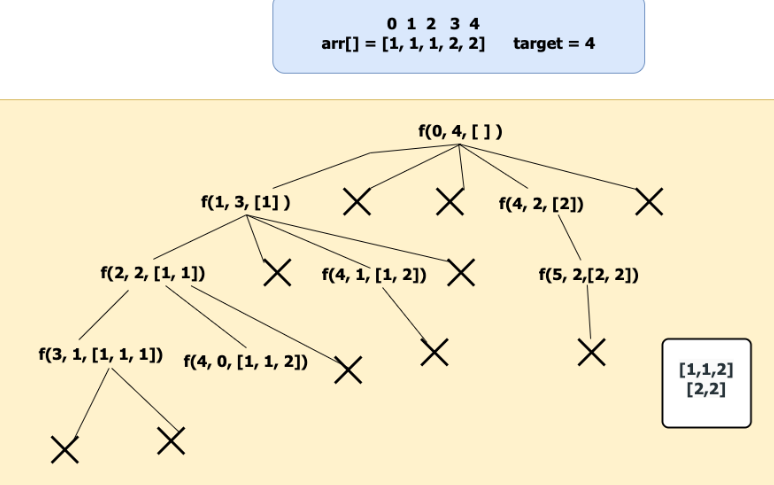
Recursive call represented for the provided example below:

Code

C++

from typing import List




def combinationSum2(candidates: List[int], target: int) -> List[List[int]]:
    ans = []
    ds = []
    candidates.sort()


    def findCombination(ind: int, target: int):
        if target == 0:
            ans.append(ds[:])
            return
        for i in range(ind, len(candidates)):
            if i > ind and candidates[i] == candidates[i - 1]:
                continue
            if candidates[i] > target:
                break
            ds.append(candidates[i])
            findCombination(i + 1, target - candidates[i])
            ds.pop()


    findCombination(0, target)
    return ans




if __name__ == "__main__":
    v = [10, 1, 2, 7, 6, 1, 5]
    comb = combinationSum2(v, 8)
    print(*comb)

Java

import java.util.*;
class TUF {
    static void findCombinations(int ind, int[] arr, int target, List < List < Integer >> ans, List < Integer > ds) {
        if (target == 0) {
            ans.add(new ArrayList < > (ds));
            return;
        }

        for (int i = ind; i < arr.length; i++) {
            if (i > ind && arr[i] == arr[i - 1]) continue;
            if (arr[i] > target) break;

            ds.add(arr[i]);
            findCombinations(i + 1, arr, target - arr[i], ans, ds);
            ds.remove(ds.size() - 1);
        }
    }
    public static List < List < Integer >> combinationSum2(int[] candidates, int target) {
        List < List < Integer >> ans = new ArrayList < > ();
        Arrays.sort(candidates);
        findCombinations(0, candidates, target, ans, new ArrayList < > ());
        return ans;
    }

    public static void main(String args[]) {
        int v[]={10,1,2,7,6,1,5};
        List < List < Integer >> comb = combinationSum2(v, 8);
        System.out.println(comb.toString().replace(",", " "));
    }
}

Python

from typing import List




def combinationSum2(candidates: List[int], target: int) -> List[List[int]]:
    ans = []
    ds = []
    candidates.sort()


    def findCombination(ind: int, target: int):
        if target == 0:
            ans.append(ds[:])
            return
        for i in range(ind, len(candidates)):
            if i > ind and candidates[i] == candidates[i - 1]:
                continue
            if candidates[i] > target:
                break
            ds.append(candidates[i])
            findCombination(i + 1, target - candidates[i])
            ds.pop()


    findCombination(0, target)
    return ans




if __name__ == "__main__":
    v = [10, 1, 2, 7, 6, 1, 5]
    comb = combinationSum2(v, 8)
    print(*comb)

Output:

[ [ 1 1 6 ][ 1 2 5 ][ 1 7 ][ 2 6 ] ]

Time Complexity:O(2^n*k)

Space Complexity:O(k*x)