What is this problem with N-Queen?
Placing N chess queens on a NĂ—N chessboard without any queens attacking one another is known as the N Queen problem.

For example, the following is a solution for the 4 Queen problem.

The anticipated result takes the shape of a matrix with “Qs” for the blocks containing queens and “.” for the empty spaces. For instance, the output matrix for the 4-Queen solution mentioned above looks like this.
. Q . .
. . . Q
Q . . .
. . Q . N Queen Problem using Backtracking:
Starting with the leftmost column, the queens are supposed to be arranged one after the other in various columns. We look for conflicts with other queens before positioning a queen in a column. We mark a row and column in the current column as part of the solution if we locate a row for which there is no collision. We go back and return false if we are unable to locate such a row because of clashes.
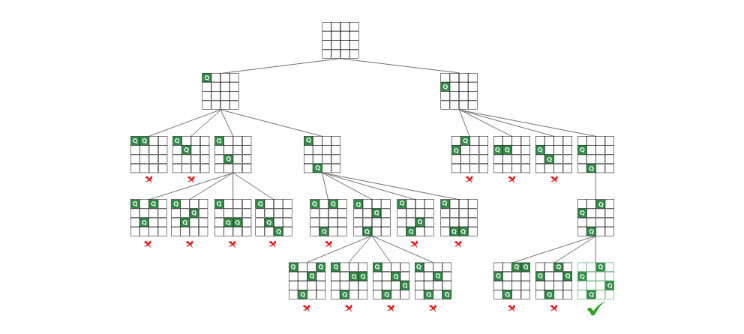
To put the concept into practice, take the actions listed below:
- Start in the column on the left.
- Return true if every queen is positioned.
- In the current column, try every row. For each row, complete the following.
- Mark this [row, column] as a component of the solution if the queen can be securely positioned here, and then recursively determine whether doing so results in a solution.
- Return true if putting the queen in [row, column] results in a solution.
- Unmark this [row, column] and go back and try other rows if positioning the queen doesn’t result in a solution.
- Return false to start retracing if every row has been tried and no workable solution has been discovered.
C++
#include <bits/stdc++.h>
using namespace std;
// A utility function to print solution
void printSolution(vector<vector<int>>& board) {
int n = board.size();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
if(board[i][j])
cout << "Q ";
else
cout << ". ";
cout << "\n";
}
}
// A utility function to check if a queen can
// be placed on board[row][col]. Note that this
// function is called when "col" queens are
// already placed in columns from 0 to col -1.
// So we need to check only left side for
// attacking queens
bool isSafe(vector<vector<int>>& board,
int row, int col) {
int n = board.size();
int i, j;
// Check this row on left side
for (i = 0; i < col; i++)
if (board[row][i])
return false;
// Check upper diagonal on left side
for (i = row, j = col; i >= 0 &&
j >= 0; i--, j--)
if (board[i][j])
return false;
// Check lower diagonal on left side
for (i = row, j = col; j >= 0 &&
i < n; i++, j--)
if (board[i][j])
return false;
return true;
}
// A recursive utility function to solve N
// Queen problem
bool solveNQUtil(vector<vector<int>>& board, int col) {
int n = board.size();
// base case: If all queens are placed
// then return true
if (col >= n)
return true;
// Consider this column and try placing
// this queen in all rows one by one
for (int i = 0; i < n; i++) {
// Check if the queen can be placed on
// board[i][col]
if (isSafe(board, i, col)) {
// Place this queen in board[i][col]
board[i][col] = 1;
// recur to place rest of the queens
if (solveNQUtil(board, col + 1))
return true;
// If placing queen in board[i][col]
// doesn't lead to a solution, then
// remove queen from board[i][col]
board[i][col] = 0; // BACKTRACK
}
}
// If the queen cannot be placed in any row in
// this column col then return false
return false;
}
// This function solves the N Queen problem using
// Backtracking. It mainly uses solveNQUtil() to
// solve the problem. It returns false if queens
// cannot be placed, otherwise, return true and
// prints placement of queens in the form of 1s.
// Please note that there may be more than one
// solutions, this function prints one of the
// feasible solutions.
bool solveNQ(int n) {
vector<vector<int>> board(n, vector<int>(n, 0));
if (solveNQUtil(board, 0) == false) {
cout << "Solution does not exist";
return false;
}
printSolution(board);
return true;
}
// Driver program to test above function
int main() {
int n = 4;
solveNQ(n);
return 0;
}C
// C program to solve N Queen Problem using backtracking
#define N 4
#include <stdbool.h>
#include <stdio.h>
// A utility function to print solution
void printSolution(int board[N][N])
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if(board[i][j])
printf("Q ");
else
printf(". ");
}
printf("\n");
}
}
// A utility function to check if a queen can
// be placed on board[row][col]. Note that this
// function is called when "col" queens are
// already placed in columns from 0 to col -1.
// So we need to check only left side for
// attacking queens
bool isSafe(int board[N][N], int row, int col)
{
int i, j;
// Check this row on left side
for (i = 0; i < col; i++)
if (board[row][i])
return false;
// Check upper diagonal on left side
for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j])
return false;
// Check lower diagonal on left side
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j])
return false;
return true;
}
// A recursive utility function to solve N
// Queen problem
bool solveNQUtil(int board[N][N], int col)
{
// Base case: If all queens are placed
// then return true
if (col >= N)
return true;
// Consider this column and try placing
// this queen in all rows one by one
for (int i = 0; i < N; i++) {
// Check if the queen can be placed on
// board[i][col]
if (isSafe(board, i, col)) {
// Place this queen in board[i][col]
board[i][col] = 1;
// Recur to place rest of the queens
if (solveNQUtil(board, col + 1))
return true;
// If placing queen in board[i][col]
// doesn't lead to a solution, then
// remove queen from board[i][col]
board[i][col] = 0; // BACKTRACK
}
}
// If the queen cannot be placed in any row in
// this column col then return false
return false;
}
// This function solves the N Queen problem using
// Backtracking. It mainly uses solveNQUtil() to
// solve the problem. It returns false if queens
// cannot be placed, otherwise, return true and
// prints placement of queens in the form of 1s.
// Please note that there may be more than one
// solutions, this function prints one of the
// feasible solutions.
bool solveNQ()
{
int board[N][N] = { { 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 } };
if (solveNQUtil(board, 0) == false) {
printf("Solution does not exist");
return false;
}
printSolution(board);
return true;
}
// Driver program to test above function
int main()
{
solveNQ();
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)Java
// Java program to solve N Queen Problem using backtracking
public class NQueenProblem {
final int N = 4;
// A utility function to print solution
void printSolution(int board[][])
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (board[i][j] == 1)
System.out.print("Q ");
else
System.out.print(". ");
}
System.out.println();
}
}
// A utility function to check if a queen can
// be placed on board[row][col]. Note that this
// function is called when "col" queens are already
// placeed in columns from 0 to col -1. So we need
// to check only left side for attacking queens
boolean isSafe(int board[][], int row, int col)
{
int i, j;
// Check this row on left side
for (i = 0; i < col; i++)
if (board[row][i] == 1)
return false;
// Check upper diagonal on left side
for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j] == 1)
return false;
// Check lower diagonal on left side
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j] == 1)
return false;
return true;
}
// A recursive utility function to solve N
// Queen problem
boolean solveNQUtil(int board[][], int col)
{
// Base case: If all queens are placed
// then return true
if (col >= N)
return true;
// Consider this column and try placing
// this queen in all rows one by one
for (int i = 0; i < N; i++) {
// Check if the queen can be placed on
// board[i][col]
if (isSafe(board, i, col)) {
// Place this queen in board[i][col]
board[i][col] = 1;
// Recur to place rest of the queens
if (solveNQUtil(board, col + 1) == true)
return true;
// If placing queen in board[i][col]
// doesn't lead to a solution then
// remove queen from board[i][col]
board[i][col] = 0; // BACKTRACK
}
}
// If the queen can not be placed in any row in
// this column col, then return false
return false;
}
// This function solves the N Queen problem using
// Backtracking. It mainly uses solveNQUtil () to
// solve the problem. It returns false if queens
// cannot be placed, otherwise, return true and
// prints placement of queens in the form of 1s.
// Please note that there may be more than one
// solutions, this function prints one of the
// feasible solutions.
boolean solveNQ()
{
int board[][] = { { 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 } };
if (solveNQUtil(board, 0) == false) {
System.out.print("Solution does not exist");
return false;
}
printSolution(board);
return true;
}
// Driver program to test above function
public static void main(String args[])
{
NQueenProblem Queen = new NQueenProblem();
Queen.solveNQ();
}
}
// This code is contributed by Abhishek ShankhadharPython
# Python3 program to solve N Queen
# Problem using backtracking
global N
N = 4
def printSolution(board):
for i in range(N):
for j in range(N):
if board[i][j] == 1:
print("Q",end=" ")
else:
print(".",end=" ")
print()
# A utility function to check if a queen can
# be placed on board[row][col]. Note that this
# function is called when "col" queens are
# already placed in columns from 0 to col -1.
# So we need to check only left side for
# attacking queens
def isSafe(board, row, col):
# Check this row on left side
for i in range(col):
if board[row][i] == 1:
return False
# Check upper diagonal on left side
for i, j in zip(range(row, -1, -1),
range(col, -1, -1)):
if board[i][j] == 1:
return False
# Check lower diagonal on left side
for i, j in zip(range(row, N, 1),
range(col, -1, -1)):
if board[i][j] == 1:
return False
return True
def solveNQUtil(board, col):
# Base case: If all queens are placed
# then return true
if col >= N:
return True
# Consider this column and try placing
# this queen in all rows one by one
for i in range(N):
if isSafe(board, i, col):
# Place this queen in board[i][col]
board[i][col] = 1
# Recur to place rest of the queens
if solveNQUtil(board, col + 1) == True:
return True
# If placing queen in board[i][col
# doesn't lead to a solution, then
# queen from board[i][col]
board[i][col] = 0
# If the queen can not be placed in any row in
# this column col then return false
return False
# This function solves the N Queen problem using
# Backtracking. It mainly uses solveNQUtil() to
# solve the problem. It returns false if queens
# cannot be placed, otherwise return true and
# placement of queens in the form of 1s.
# note that there may be more than one
# solutions, this function prints one of the
# feasible solutions.
def solveNQ():
board = [[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]]
if solveNQUtil(board, 0) == False:
print("Solution does not exist")
return False
printSolution(board)
return True
# Driver Code
if __name__ == '__main__':
solveNQ()
# This code is contributed by Divyanshu MehtaC#
// C# program to solve N Queen Problem
// using backtracking
using System;
class GFG
{
readonly int N = 4;
// A utility function to print solution
void printSolution(int [,]board)
{
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
if (board[i, j] == 1)
Console.Write("Q ");
else
Console.Write(". ");
}
Console.WriteLine();
}
}
// A utility function to check if a queen can
// be placed on board[row,col]. Note that this
// function is called when "col" queens are already
// placeed in columns from 0 to col -1. So we need
// to check only left side for attacking queens
bool isSafe(int [,]board, int row, int col)
{
int i, j;
// Check this row on left side
for (i = 0; i < col; i++)
if (board[row,i] == 1)
return false;
// Check upper diagonal on left side
for (i = row, j = col; i >= 0 &&
j >= 0; i--, j--)
if (board[i,j] == 1)
return false;
// Check lower diagonal on left side
for (i = row, j = col; j >= 0 &&
i < N; i++, j--)
if (board[i, j] == 1)
return false;
return true;
}
// A recursive utility function to solve N
// Queen problem
bool solveNQUtil(int [,]board, int col)
{
// Base case: If all queens are placed
// then return true
if (col >= N)
return true;
// Consider this column and try placing
// this queen in all rows one by one
for (int i = 0; i < N; i++)
{
// Check if the queen can be placed on
// board[i,col]
if (isSafe(board, i, col))
{
// Place this queen in board[i,col]
board[i, col] = 1;
// Recur to place rest of the queens
if (solveNQUtil(board, col + 1) == true)
return true;
// If placing queen in board[i,col]
// doesn't lead to a solution then
// remove queen from board[i,col]
board[i, col] = 0; // BACKTRACK
}
}
// If the queen can not be placed in any row in
// this column col, then return false
return false;
}
// This function solves the N Queen problem using
// Backtracking. It mainly uses solveNQUtil () to
// solve the problem. It returns false if queens
// cannot be placed, otherwise, return true and
// prints placement of queens in the form of 1s.
// Please note that there may be more than one
// solutions, this function prints one of the
// feasible solutions.
bool solveNQ()
{
int [,]board = {{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 }};
if (solveNQUtil(board, 0) == false)
{
Console.Write("Solution does not exist");
return false;
}
printSolution(board);
return true;
}
// Driver Code
public static void Main(String []args)
{
GFG Queen = new GFG();
Queen.solveNQ();
}
}
// This code is contributed by Princi SinghTime Complexity:Â O(N!)
Auxiliary Space:Â O(N2)
