Print all matrix elements in spiral form given a matrix mat[][] with dimensions m x n.
Here are some examples:
Input: mat[][] = [[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]]
Output: 1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10
Explanation: The output is matrix in spiral format. 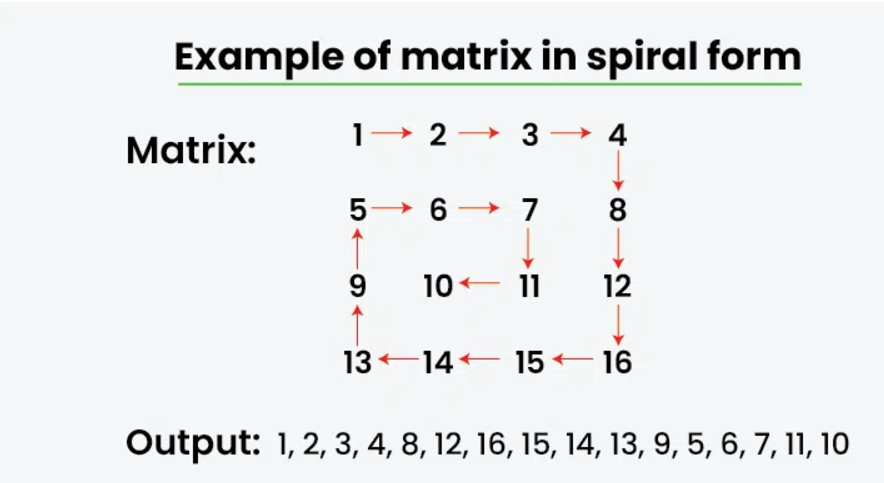
Input: mat[][]= [[1, 2, 3, 4, 5, 6],
[7, 8, 9, 10, 11, 12],
[13, 14, 15, 16, 17, 18]]
Output: 1 2 3 4 5 6 12 18 17 16 15 14 13 7 8 9 10 11
Explanation: The output is matrix in spiral format.
Table of Content
- [Naive Approach]: Using Simulation by Visited Matrix – O(m*n) Time and O(m*n) Space
- [Space Optimized Approach]: Using Boundary Traversal – O(m*n) Time and O(1) Space
[Naive Approach]: Using Simulation by Visited Matrix – O(m*n) Time and O(m*n) Space
Marking the cells that have already been visited helps one to replicate the spiral travel. The movement (right, down, left, up) can be tracked using a direction array; when we come upon a visited cell or the border, we can modify direction.
- Create a 2D array visible to record visited cells initially.
- To depict right, down, left, and upward motions, use direction arrays dr and dc.
- Starting from the top-left cell, follow the direction arrays to see every cell.
- Change orientation upon coming upon a visited cell or a boundary.
- Go on until every cell has been seen.
C++
//C++ program to perform spiral order
// traversal of a matrix
#include <bits/stdc++.h>
using namespace std;
vector<int> spiralOrder(vector<vector<int> >& mat) {
// Number of rows in the matrix
int m = mat.size();
// Number of columns in the matrix
int n = mat[0].size();
// Vector to store the spiral order elements
vector<int> result;
// Edge case: if matrix is empty
if (m == 0)
return result;
// 2D vector to keep track of visited cells
vector<vector<bool> > vis(m, vector<bool>(n, false));
// Arrays to represent the four possible movement
// directions: right, down, left, up
// Change in row index for each direction
int dr[] = { 0, 1, 0, -1 };
// Change in column index for each direction
int dc[] = { 1, 0, -1, 0 };
// Initial position in the matrix
int r = 0, c = 0;
// Initial direction index (0 corresponds to 'right')
int di = 0;
// Iterate through all elements in the matrix
for (int i = 0; i < m * n; ++i) {
// Add current element to result vector
result.push_back(mat[r][c]);
// Mark current cell as visited
vis[r][c] = true;
// Calculate the next cell coordinates based on
// current direction
int newR = r + dr[di];
int newC = c + dc[di];
// Check if the next cell is within bounds and not
// visited
if (0 <= newR && newR < m && 0 <= newC && newC < n
&& !vis[newR][newC]) {
// Move to the next row
r = newR;
// Move to the next column
c = newC;
}
else {
// Change direction (turn clockwise)
di = (di + 1) % 4;
// Move to the next row according to new
// direction
r += dr[di];
// Move to the next column according to new
// direction
c += dc[di];
}
}
// Return the vector containing spiral order elements
return result;
}
int main() {
vector<vector<int> > mat = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 } };
vector<int> result = spiralOrder(mat);
for (int num : result) {
cout << num << " ";
}
return 0;
}
Java
//Java program to perform spiral order
// traversal of a matrix
import java.util.*;
class GfG {
static List<Integer> spiralOrder(int[][] mat) {
// Number of rows in the matrix
int m = mat.length;
// Number of columns in the matrix
int n = mat[0].length;
// List to store the spiral order elements
List<Integer> result = new ArrayList<>();
// Edge case: if matrix is empty
if (m == 0)
return result;
// 2D array to keep track of visited cells
boolean[][] vis = new boolean[m][n];
// Arrays to represent the four possible movement
// directions: right, down, left, up
// Change in row index for each direction
int[] dr = {0, 1, 0, -1};
// Change in column index for each direction
int[] dc = {1, 0, -1, 0};
// Initial position in the matrix
int r = 0, c = 0;
// Initial direction index (0 corresponds to 'right')
int di = 0;
// Iterate through all elements in the matrix
for (int i = 0; i < m * n; ++i) {
// Add current element to result list
result.add(mat[r][c]);
// Mark current cell as visited
vis[r][c] = true;
// Calculate the next cell coordinates based on
// current direction
int newR = r + dr[di];
int newC = c + dc[di];
// Check if the next cell is within bounds and not
// visited
if (0 <= newR && newR < m && 0 <= newC && newC < n
&& !vis[newR][newC]) {
// Move to the next row
r = newR;
// Move to the next column
c = newC;
} else {
// Change direction (turn clockwise)
di = (di + 1) % 4;
// Move to the next row according to new
// direction
r += dr[di];
// Move to the next column according to new
// direction
c += dc[di];
}
}
// Return the list containing spiral order elements
return result;
}
public static void main(String[] args) {
int[][] mat = {
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 }
};
List<Integer> result = spiralOrder(mat);
for (int num : result) {
System.out.print(num + " ");
}
}
}Python
# Python program to perform spiral order
# traversal of a matrix
def spiralOrder(matrix):
# Number of rows in the matrix
m = len(mat)
# Number of columns in the matrix
n = len(mat[0])
# List to store the spiral order elements
result = []
# Edge case: if matrix is empty
if m == 0:
return result
# List to keep track of visited cells
vis = [[False] * n for _ in range(m)]
# Arrays to represent the four possible movement
# directions: right, down, left, up
# Change in row index for each direction
dr = [0, 1, 0, -1]
# Change in column index for each direction
dc = [1, 0, -1, 0]
# Initial position in the matrix
r, c = 0, 0
# Initial direction index (0 corresponds to 'right')
di = 0
# Iterate through all elements in the matrix
for i in range(m * n):
# Add current element to result list
result.append(mat[r][c])
# Mark current cell as visited
vis[r][c] = True
# Calculate the next cell coordinates based on
# current direction
newR, newC = r + dr[di], c + dc[di]
# Check if the next cell is within bounds and not
# visited
if 0 <= newR < m and 0 <= newC < n and not vis[newR][newC]:
# Move to the next row
r, c = newR, newC
else:
# Change direction (turn clockwise)
di = (di + 1) % 4
# Move to the next row according to new
# direction
r += dr[di]
# Move to the next column according to new
# direction
c += dc[di]
# Return the list containing spiral order elements
return result
if __name__ == "__main__":
mat = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]
]
result = spiralOrder(mat)
print(result)C#
// C# program to perform spiral order
// traversal of a matrix
using System;
using System.Collections.Generic;
class GfG {
static List<int> SpiralOrder(int[,] mat) {
// Number of rows in the matrix
int m = mat.GetLength(0);
// Number of columns in the matrix
int n = mat.GetLength(1);
// List to store the spiral order elements
List<int> result = new List<int>();
// Edge case: if matrix is empty
if (m == 0)
return result;
// 2D array to keep track of visited cells
bool[,] vis = new bool[m, n];
// Arrays to represent the four possible movement
// directions: right, down, left, up
// Change in row index for each direction
int[] dr = { 0, 1, 0, -1 };
// Change in column index for each direction
int[] dc = { 1, 0, -1, 0 };
// Initial position in the matrix
int r = 0, c = 0;
// Initial direction index (0 corresponds to 'right')
int di = 0;
// Iterate through all elements in the matrix
for (int i = 0; i < m * n; ++i) {
// Add current element to result list
result.Add(mat[r, c]);
// Mark current cell as visited
vis[r, c] = true;
// Calculate the next cell coordinates based on
// current direction
int newR = r + dr[di];
int newC = c + dc[di];
// Check if the next cell is within bounds and not
// visited
if (0 <= newR && newR < m && 0 <= newC && newC < n
&& !vis[newR, newC]) {
// Move to the next row
r = newR;
// Move to the next column
c = newC;
}
else {
// Change direction (turn clockwise)
di = (di + 1) % 4;
// Move to the next row according to new
// direction
r += dr[di];
// Move to the next column according to new
// direction
c += dc[di];
}
}
// Return the list containing spiral
// order elements
return result;
}
static void Main() {
int[,] mat = {
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 }
};
List<int> result = SpiralOrder(mat);
foreach (int num in result) {
Console.Write(num + " ");
}
}
}JavaScript
// Javascript program to perform spiral order
// traversal of a matrix
function spiralOrder(mat) {
// Number of rows in the matrix
let m = mat.length;
// Number of columns in the matrix
let n = mat[0].length;
// Array to store the spiral order elements
let result = [];
// Edge case: if matrix is empty
if (m === 0)
return result;
// 2D array to keep track of visited cells
let vis = Array.from({length : m},
() => Array(n).fill(false));
// Arrays to represent the four possible movement
// directions: right, down, left, up
// Change in row index for each direction
let dr = [ 0, 1, 0, -1 ];
// Change in column index for each direction
let dc = [ 1, 0, -1, 0 ];
// Initial position in the matrix
let r = 0, c = 0;
// Initial direction index (0 corresponds to 'right')
let di = 0;
// Iterate through all elements in the matrix
for (let i = 0; i < m * n; ++i) {
// Add current element to result array
result.push(mat[r][c]);
// Mark current cell as visited
vis[r][c] = true;
// Calculate the next cell coordinates based on
// current direction
let newR = r + dr[di];
let newC = c + dc[di];
// Check if the next cell is within bounds and not
// visited
if (0 <= newR && newR < m && 0 <= newC && newC < n
&& !vis[newR][newC]) {
// Move to the next row
r = newR;
// Move to the next column
c = newC;
}
else {
// Change direction (turn clockwise)
di = (di + 1) % 4;
// Move to the next row according to new
// direction
r += dr[di];
// Move to the next column according to new
// direction
c += dc[di];
}
}
// Return the array containing spiral
// order elements
return result;
}
let mat = [
[ 1, 2, 3, 4 ], [ 5, 6, 7, 8 ], [ 9, 10, 11, 12 ],
[ 13, 14, 15, 16 ]
];
let result = spiralOrder(mat);
console.log(result.join(" "));Output
1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10
Time Complexity: O(m*n), where m and n are the number of rows and columns of the given matrix respectively.
Auxiliary Space: O(m*n), for the seen matrix and the result vector.
