The challenge is to combine all the overlapping intervals into one and produce the output which should include only mutually exclusive intervals given an array of time intervals whereby arr[i] = [starti, endi].
As an illustration,:
Input: arr[] = [[1, 3], [2, 4], [6, 8], [9, 10]]
Output: [[1, 4], [6, 8], [9, 10]]
Explanation: In the given intervals, we have only two overlapping intervals [1, 3] and [2, 4]. Therefore, we will merge these two and return [[1, 4]], [6, 8], [9, 10]].
Input: arr[] = [[7, 8], [1, 5], [2, 4], [4, 6]]
Output: [[1, 6], [7, 8]]
Explanation: We will merge the overlapping intervals [[1, 5], [2, 4], [4, 6]] into a single interval [1, 6].Table of Content
- [Naive Approach] Checking All Possible Overlaps – O(n^2) Time and O(1) Space
- [Expected Approach] Checking Last Merged Interval – O(n*log(n)) Time and O(n) Space
[Naive Approach] Checking All Possible Overlaps – O(n^2) Time and O(1) Space
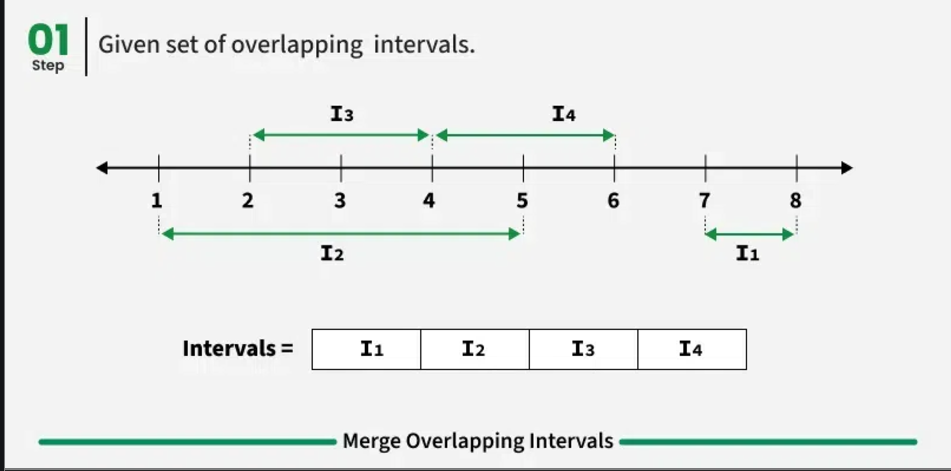
One might start from the first interval and compare it with every other interval for overlaps by first grouping all the intervals and then. Eliminate the other interval from the list and combine the other into the first interval if the first interval crosses any other interval. Proceed similarly for the next intervals following the first.
C++
// C++ Code to Merge Overlapping Intervals by Checking
// All Possible Overlaps
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> mergeOverlap(vector<vector<int>> &arr) {
int n = arr.size();
sort(arr.begin(), arr.end());
vector<vector<int>> res;
// Checking for all possible overlaps
for (int i = 0; i < n; i++) {
int start = arr[i][0];
int end = arr[i][1];
// Skipping already merged intervals
if (!res.empty() && res.back()[1] >= end)
continue;
// Find the end of the merged range
for (int j = i + 1; j < n; j++) {
if (arr[j][0] <= end)
end = max(end, arr[j][1]);
}
res.push_back({start, end});
}
return res;
}
int main() {
vector<vector<int>> arr = {{7, 8}, {1, 5}, {2, 4}, {4, 6}};
vector<vector<int>> res = mergeOverlap(arr);
for (auto interval : res)
cout << interval[0] << " " << interval[1] << endl;
return 0;
}
Java
// Java Code to Merge Overlapping Intervals by Checking
// All Possible Overlaps
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
class GfG {
static List<int[]> mergeOverlap(int[][] arr) {
int n = arr.length;
Arrays.sort(arr, (a, b) -> Integer.compare(a[0], b[0]));
List<int[]> res = new ArrayList<>();
// Checking for all possible overlaps
for (int i = 0; i < n; i++) {
int start = arr[i][0];
int end = arr[i][1];
// Skipping already merged intervals
if (!res.isEmpty() && res.get(res.size() - 1)[1] >= end) {
continue;
}
// Find the end of the merged range
for (int j = i + 1; j < n; j++) {
if (arr[j][0] <= end) {
end = Math.max(end, arr[j][1]);
}
}
res.add(new int[]{start, end});
}
return res;
}
public static void main(String[] args) {
int[][] arr = {{7, 8}, {1, 5}, {2, 4}, {4, 6}};
List<int[]> res = mergeOverlap(arr);
for (int[] interval : res) {
System.out.println(interval[0] + " " + interval[1]);
}
}
}Python
# Python Code to Merge Overlapping Intervals by Checking
# All Possible Overlaps
def mergeOverlap(arr):
n = len(arr)
arr.sort()
res = []
# Checking for all possible overlaps
for i in range(n):
start = arr[i][0]
end = arr[i][1]
# Skipping already merged intervals
if res and res[-1][1] >= end:
continue
# Find the end of the merged range
for j in range(i + 1, n):
if arr[j][0] <= end:
end = max(end, arr[j][1])
res.append([start, end])
return res
if __name__ == "__main__":
arr = [[7, 8], [1, 5], [2, 4], [4, 6]]
res = mergeOverlap(arr)
for interval in res:
print(interval[0], interval[1])C#
// C# Code to Merge Overlapping Intervals by Checking
// All Possible Overlaps
using System;
using System.Collections.Generic;
class GfG {
static List<int[]> mergeOverlap(int[][] arr) {
int n = arr.Length;
Array.Sort(arr, (a, b) => a[0].CompareTo(b[0]));
List<int[]> res = new List<int[]>();
// Checking for all possible overlaps
for (int i = 0; i < n; i++) {
int start = arr[i][0];
int end = arr[i][1];
// Skipping already merged intervals
if (res.Count > 0 && res[res.Count - 1][1] >= end)
continue;
// Find the end of the merged range
for (int j = i + 1; j < n; j++) {
if (arr[j][0] <= end)
end = Math.Max(end, arr[j][1]);
}
res.Add(new int[] { start, end });
}
return res;
}
static void Main() {
int[][] arr = new int[][] {
new int[] { 7, 8 },
new int[] { 1, 5 },
new int[] { 2, 4 },
new int[] { 4, 6 }
};
List<int[]> res = mergeOverlap(arr);
foreach (var interval in res)
Console.WriteLine($"{interval[0]} {interval[1]}");
}
}JavaScript
// JavaScript Code to Merge Overlapping Intervals by Checking
// All Possible Overlaps
function mergeOverlap(arr) {
let n = arr.length;
arr.sort((a, b) => a[0] - b[0]);
let res = [];
// Checking for all possible overlaps
for (let i = 0; i < n; i++) {
let start = arr[i][0];
let end = arr[i][1];
// Skipping already merged intervals
if (res.length > 0 && res[res.length - 1][1] >= end) {
continue;
}
// Find the end of the merged range
for (let j = i + 1; j < n; j++) {
if (arr[j][0] <= end) {
end = Math.max(end, arr[j][1]);
}
}
res.push([start, end]);
}
return res;
}
const arr = [[7, 8], [1, 5], [2, 4], [4, 6]];
const res = mergeOverlap(arr);
for (const interval of res)
console.log(interval[0], interval[1]);Output
1 6 7 8
