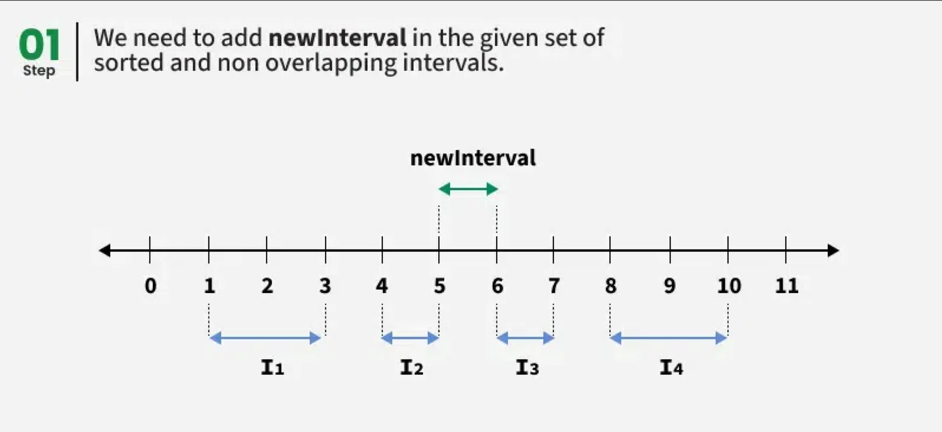
A new interval we add could intersect some adjacent intervals in the array. Given the already sorted interval array, one can find overlapping intervals in a contiguous subarray. We identify overlapping interval’s subarray and combine them with new interval to generate a single merged interval.
We first add the lower intervals, then this merged interval, and lastly the remaining intervals in the output to preserve the order ordered.
C++
// C++ program to insert a new Interval in an array of sorted and
// non-overlapping interval using Contiguous Interval Merging
#include <iostream>
#include <vector>
using namespace std;
// Function to insert and merge intervals
vector<vector<int>> insertInterval(vector<vector<int>>& intervals,
vector<int> &newInterval) {
vector<vector<int>> res;
int i = 0;
int n = intervals.size();
// Add all intervals that come before the new interval
while (i < n && intervals[i][1] < newInterval[0]) {
res.push_back(intervals[i]);
i++;
}
// Merge all overlapping intervals with the new interval
while (i < n && intervals[i][0] <= newInterval[1]) {
newInterval[0] = min(newInterval[0], intervals[i][0]);
newInterval[1] = max(newInterval[1], intervals[i][1]);
i++;
}
res.push_back(newInterval);
// Add all the remaining intervals
while (i < n) {
res.push_back(intervals[i]);
i++;
}
return res;
}
int main() {
vector<vector<int>> intervals = {{1, 3}, {4, 5}, {6, 7}, {8, 10}};
vector<int> newInterval = {5, 6};
vector<vector<int>> res = insertInterval(intervals, newInterval);
for (vector<int> interval: res) {
cout << interval[0] << " " << interval[1] << "\n";
}
return 0;
}Java
// Java program to insert a new Interval in an array of sorted and
// non-overlapping interval using Contiguous Interval Merging
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
class GfG {
// Function to insert and merge intervals
static ArrayList<int[]> insertInterval(int[][] intervals, int[] newInterval) {
ArrayList<int[]> res = new ArrayList<>();
int i = 0;
int n = intervals.length;
// Add all intervals that come before the new interval
while (i < n && intervals[i][1] < newInterval[0]) {
res.add(intervals[i]);
i++;
}
// Merge all overlapping intervals with the new interval
while (i < n && intervals[i][0] <= newInterval[1]) {
newInterval[0] = Math.min(newInterval[0], intervals[i][0]);
newInterval[1] = Math.max(newInterval[1], intervals[i][1]);
i++;
}
res.add(newInterval);
// Add all the remaining intervals
while (i < n) {
res.add(intervals[i]);
i++;
}
// Return the result as a List<int[]>
return res;
}
public static void main(String[] args) {
int[][] intervals = {{1, 3}, {4, 5}, {6, 7}, {8, 10}};
int[] newInterval = {5, 6};
ArrayList<int[]> res = insertInterval(intervals, newInterval);
for (int[] interval : res) {
System.out.println(interval[0] + " " + interval[1]);
}
}
}Python
# Python program to insert a new Interval in an array of sorted and
# non-overlapping interval using Contiguous Interval Merging
# Function to insert and merge intervals
def insertInterval(intervals, newInterval):
res = []
i = 0
n = len(intervals)
# Add all intervals that come before the new interval
while i < n and intervals[i][1] < newInterval[0]:
res.append(intervals[i])
i += 1
# Merge all overlapping intervals with the new interval
while i < n and intervals[i][0] <= newInterval[1]:
newInterval[0] = min(newInterval[0], intervals[i][0])
newInterval[1] = max(newInterval[1], intervals[i][1])
i += 1
res.append(newInterval)
# Add all the remaining intervals
while i < n:
res.append(intervals[i])
i += 1
return res
if __name__ == "__main__":
intervals = [[1, 3], [4, 5], [6, 7], [8, 10]]
newInterval = [5, 6]
res = insertInterval(intervals, newInterval)
for interval in res:
print(interval[0], interval[1])C#
// C# program to insert a new Interval in an array of sorted and
// non-overlapping interval using Contiguous Interval Merging
using System;
using System.Collections.Generic;
class GfG {
// Function to insert and merge intervals
static List<int[]> insertInterval(int[][] intervals, int[] newInterval) {
List<int[]> res = new List<int[]>();
int i = 0;
int n = intervals.Length;
// Add all intervals that come before the new interval
while (i < n && intervals[i][1] < newInterval[0]) {
res.Add(intervals[i]);
i++;
}
// Merge all overlapping intervals with the new interval
while (i < n && intervals[i][0] <= newInterval[1]) {
newInterval[0] = Math.Min(newInterval[0], intervals[i][0]);
newInterval[1] = Math.Max(newInterval[1], intervals[i][1]);
i++;
}
res.Add(newInterval);
// Add all the remaining intervals
while (i < n) {
res.Add(intervals[i]);
i++;
}
// Return result as List<int[]>
return res;
}
static void Main(string[] args) {
int[][] intervals = new int[][] {
new int[] {1, 3},
new int[] {4, 5},
new int[] {6, 7},
new int[] {8, 10}
};
int[] newInterval = new int[] {5, 6};
List<int[]> res = insertInterval(intervals, newInterval);
foreach (int[] interval in res) {
Console.WriteLine(interval[0] + " " + interval[1]);
}
}
}JavaScript
// Javascript program to insert a new Interval in an array of sorted and
// non-overlapping interval using Contiguous Interval Merging
function insertInterval(intervals, newInterval) {
let res = [];
let i = 0;
const n = intervals.length;
// Add all intervals that come before the new interval
while (i < n && intervals[i][1] < newInterval[0]) {
res.push(intervals[i]);
i++;
}
// Merge all overlapping intervals with the new interval
while (i < n && intervals[i][0] <= newInterval[1]) {
newInterval[0] = Math.min(newInterval[0], intervals[i][0]);
newInterval[1] = Math.max(newInterval[1], intervals[i][1]);
i++;
}
res.push(newInterval);
// Add all the remaining intervals
while (i < n) {
res.push(intervals[i]);
i++;
}
return res;
}
// Driver Code
const intervals = [[1, 3], [4, 5], [6, 7], [8, 10]];
const newInterval = [5, 6];
const res = insertInterval(intervals, newInterval);
for (const interval of res) {
console.log(interval[0] + " " + interval[1]);
};Output
1 3 4 7 8 10
