Write a function returning cost of minimum cost path to reach (M, N) from (0, 0) considering a cost matrix cost[][ and a position (M, N) in cost[][]. Every matrix cell stands for a cost to be crossed through. Including both source and destination, a path’s total cost to reach (M, N) is the sum of all the expenses on that path. From a given cell, i.e., from a given i, j, cells (i+1, j), and (i, j+1) can be navigated only down, right and diagonally lower cells.
Note: You might suppose that every expense is a positive integer.
Input
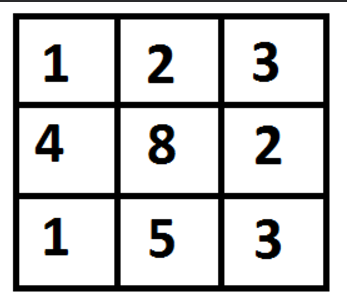
The path with minimum cost is highlighted in the following figure. The path is (0, 0) –> (0, 1) –> (1, 2) –> (2, 2). The cost of the path is 8 (1 + 2 + 2 + 3).
Output
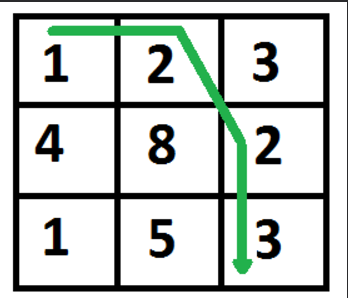
Table of Content
- Min cost path using recursion:
- Min cost path using Memoization DP:
Recursion allows a minimum cost path.
Use the below concept to address the issue:
The optimal substructure property of this issue exists. One of the three cells—either (m-1, n-1) or (m-1, n) or (m, n-1)—must be the route of reach (m, n). Minimum cost to reach (m, n) can thus be expressed as “minimum of the 3 cells plus cost[m][n]”.
min (minCost(m-1, n-1), minCost(m-1, n), minCost(m, n-1)) + cost[m][n] minCost(m, n)
C++
#include <bits/stdc++.h>
using namespace std;
// Function to return the cost of the minimum cost path
// from (0,0) to (m, n) in a cost matrix
int minCost(vector<vector<int>>& cost, int m, int n) {
if (m < 0 || n < 0)
return INT_MAX;
if (m == 0 && n == 0)
return cost[m][n];
return cost[m][n] + min({minCost(cost, m, n - 1),
minCost(cost, m - 1, n),
minCost(cost, m - 1, n - 1)});
}
// Driver code
int main() {
vector<vector<int>> cost = { { 1, 2, 3 },
{ 4, 8, 2 },
{ 1, 5, 3 } };
cout << "Minimum cost: " << minCost(cost, 2, 2) << endl;
return 0;
}C
/* A Naive recursive implementation of MCP(Minimum Cost
* Path) problem */
#include <limits.h>
#include <stdio.h>
#define R 3
#define C 3
int min(int x, int y, int z);
/* Returns cost of minimum cost path from (0,0) to (m, n) in
* mat[R][C]*/
int minCost(int cost[R][C], int m, int n)
{
if (n < 0 || m < 0)
return INT_MAX;
else if (m == 0 && n == 0)
return cost[m][n];
else
return cost[m][n]
+ min(minCost(cost, m - 1, n - 1),
minCost(cost, m - 1, n),
minCost(cost, m, n - 1));
}
/* A utility function that returns minimum of 3 integers */
int min(int x, int y, int z)
{
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
/* Driver code */
int main()
{
int cost[R][C]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
printf(" %d ", minCost(cost, 2, 2));
return 0;
}Java
/* A Naive recursive implementation of
MCP(Minimum Cost Path) problem */
public class GFG {
/* A utility function that returns
minimum of 3 integers */
static int min(int x, int y, int z)
{
if (x < y)
return (x < z) ? x : z;
else
return (y < z) ? y : z;
}
/* Returns cost of minimum cost path
from (0,0) to (m, n) in mat[R][C]*/
static int minCost(int cost[][], int m, int n)
{
if (n < 0 || m < 0)
return Integer.MAX_VALUE;
else if (m == 0 && n == 0)
return cost[m][n];
else
return cost[m][n]
+ min(minCost(cost, m - 1, n - 1),
minCost(cost, m - 1, n),
minCost(cost, m, n - 1));
}
// Driver code
public static void main(String args[])
{
int cost[][]
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
System.out.print(minCost(cost, 2, 2));
}
}
// This code is contributed by Sam007Python
# A Naive recursive implementation of MCP(Minimum Cost Path) problem
import sys
R = 3
C = 3
# Returns cost of minimum cost path from (0,0) to (m, n) in mat[R][C]
def minCost(cost, m, n):
if (n < 0 or m < 0):
return sys.maxsize
elif (m == 0 and n == 0):
return cost[m][n]
else:
return cost[m][n] + min(minCost(cost, m-1, n-1),
minCost(cost, m-1, n),
minCost(cost, m, n-1))
# A utility function that returns minimum of 3 integers */
def min(x, y, z):
if (x < y):
return x if (x < z) else z
else:
return y if (y < z) else z
# Driver code
cost = [[1, 2, 3],
[4, 8, 2],
[1, 5, 3]]
print(minCost(cost, 2, 2))
# This code is contributed by
# Smitha Dinesh SemwalC#
/* A Naive recursive implementation of
MCP(Minimum Cost Path) problem */
using System;
class GFG {
/* A utility function that
returns minimum of 3 integers */
static int min(int x, int y, int z)
{
if (x < y)
return ((x < z) ? x : z);
else
return ((y < z) ? y : z);
}
/* Returns cost of minimum
cost path from (0,0) to
(m, n) in mat[R][C]*/
static int minCost(int[, ] cost, int m, int n)
{
if (n < 0 || m < 0)
return int.MaxValue;
else if (m == 0 && n == 0)
return cost[m, n];
else
return cost[m, n]
+ min(minCost(cost, m - 1, n - 1),
minCost(cost, m - 1, n),
minCost(cost, m, n - 1));
}
// Driver code
public static void Main()
{
int[, ] cost
= { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } };
Console.Write(minCost(cost, 2, 2));
}
}
// This code is contributed
// by shiv_bhakt.JavaScript
function minCost(cost, m, n) {
if (m < 0 || n < 0) {
return Number.MAX_SAFE_INTEGER;
}
if (m === 0 && n === 0) {
return cost[m][n];
}
return cost[m][n] + Math.min(
minCost(cost, m, n - 1),
minCost(cost, m - 1, n),
minCost(cost, m - 1, n - 1)
);
}
// Driver code
const cost = [
[1, 2, 3],
[4, 8, 2],
[1, 5, 3]
];
console.log("Minimum cost:", minCost(cost, 2, 2));Output
8
Time Complexity: O((M * N)3)
Auxiliary Space: O(M + N), for recursive stack space
