Given pre-order and in-order traversals of a Binary Tree, the challenge is to build the tree and retrieve its root.
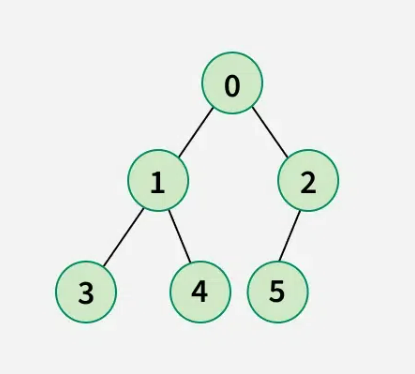
Table of Content
- [Naive Approach] Using Pre-order traversal – O(n^2) Time and O(h) Space
- [Expected Approach] Using Pre-order traversal and Hash map – O(n) Time and O(n) Space
[Naive Approach] Using Pre-order traversal – O(n^2) Time and O(h) Space
Pre-order traversal will help one build the tree. Create root node by first element of the pre-order array. In the in-order array, determine this node’s index. Create the left subtree in-order using the components on the left side of the root node. Likewise build the appropriate subtree in-order using the items on the right side of the root node.
C++
// c++ program to construct tree using
// inorder and preorder traversals
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node *left, *right;
Node(int x) {
data = x;
left = nullptr;
right = nullptr;
}
};
// Function to find the index of an element.
int searchValue(vector<int>& in, int value, int s, int e) {
for (int i=s; i<=e; i++) {
if (in[i] == value)
return i;
}
return -1;
}
// Recursive function to build the binary tree.
Node* buildTreeRecur(vector<int>& in, vector<int>& pre,
int &preIndex, int s, int e) {
// For empty array, return null
if (s > e) return nullptr;
// create the root Node
Node* root = new Node(pre[preIndex]);
preIndex++;
// find the index of first element of pre-order array
// in the in-order array.
int index = searchValue(in, pre[preIndex-1], s, e);
// Recursively create the left and right subtree.
root->left = buildTreeRecur(in, pre, preIndex, s, index-1);
root->right = buildTreeRecur(in, pre, preIndex, index+1, e);
return root;
}
Node* buildTree(vector<int>& in, vector<int>& pre) {
// Build the tree recursively.
int n = pre.size();
int preIndex = 0;
Node* root = buildTreeRecur(in, pre, preIndex, 0, n-1);
return root;
}
void printPostorder(Node* root) {
if (root == nullptr)
return;
printPostorder(root->left);
printPostorder(root->right);
cout << root->data << " ";
}
int main() {
vector<int> in = {3, 1, 4, 0, 5, 2};
vector<int> pre = {0, 1, 3, 4, 2, 5};
Node* root = buildTree(in, pre);
printPostorder(root);
return 0;
}Java
// Java program to construct tree using
// inorder and preorder traversals
class Node {
int data;
Node left, right;
Node(int x) {
data = x;
left = null;
right = null;
}
}
class GfG {
// Function to find the index of an element.
static int searchValue(int[] in, int value, int s, int e) {
for (int i = s; i <= e; i++) {
if (in[i] == value)
return i;
}
return -1;
}
// Recursive function to build the binary tree.
static Node buildTreeRecur(int[] in, int[] pre,
int[] preIndex, int s, int e) {
// For empty array, return null
if (s > e) return null;
// create the root Node
Node root = new Node(pre[preIndex[0]]);
preIndex[0]++;
// find the index of first element of pre-order array
// in the in-order array.
int index = searchValue(in, pre[preIndex[0] - 1], s, e);
// Recursively create the left and right subtree.
root.left = buildTreeRecur(in, pre, preIndex, s, index - 1);
root.right = buildTreeRecur(in, pre, preIndex, index + 1, e);
return root;
}
static Node buildTree(int[] in, int[] pre) {
int n = in.length;
// Build the tree recursively.
int[] preIndex = {0};
return buildTreeRecur(in, pre, preIndex, 0, n - 1);
}
static void printPostorder(Node root) {
if (root == null) return;
printPostorder(root.left);
printPostorder(root.right);
System.out.print(root.data + " ");
}
public static void main(String[] args) {
int[] in = {3, 1, 4, 0, 5, 2};
int[] pre = {0, 1, 3, 4, 2, 5};
Node root = buildTree(in, pre);
printPostorder(root);
}
}Python
# Python program to construct tree using
# inorder and preorder traversals
class Node:
def __init__(self, x):
self.data = x
self.left = None
self.right = None
# Function to find the index of an element.
def searchValue(inorder, value, s, e):
for i in range(s, e + 1):
if inorder[i] == value:
return i
return -1
# Recursive function to build the binary tree.
def buildTreeRecur(inorder, preorder, preIndex, s, e):
# For empty array, return None
if s > e:
return None
# create the root Node
root = Node(preorder[preIndex[0]])
preIndex[0] += 1
# find the index of first element of pre-order array
# in the in-order array.
index = searchValue(inorder, preorder[preIndex[0] - 1], s, e)
# Recursively create the left and right subtree.
root.left = buildTreeRecur(inorder, preorder, \
preIndex, s, index - 1)
root.right = buildTreeRecur(inorder, preorder, \
preIndex, index + 1, e)
return root
def buildTree(inorder, preorder):
n = len(inorder)
# Build the tree recursively.
preIndex = [0]
return buildTreeRecur(inorder, preorder,\
preIndex, 0, n - 1)
def printPostorder(root):
if root is None:
return
printPostorder(root.left)
printPostorder(root.right)
print(root.data, end=" ")
inorder = [3, 1, 4, 0, 5, 2]
preorder = [0, 1, 3, 4, 2, 5]
root = buildTree(inorder, preorder)
printPostorder(root)C#
// C# program to construct tree using
// inorder and preorder traversals
using System;
using System.Collections.Generic;
class Node {
public int data;
public Node left, right;
public Node(int x) {
data = x;
left = null;
right = null;
}
}
class GfG {
// Function to find the index of an element.
static int SearchValue(List<int> inorder,
int value, int s, int e) {
for (int i = s; i <= e; i++) {
if (inorder[i] == value)
return i;
}
return -1;
}
// Recursive function to build the binary tree.
static Node BuildTreeRecur(List<int> inorder,
List<int> preorder, ref int preIndex, int s, int e) {
// For empty array, return null
if (s > e) return null;
// create the root Node
Node root = new Node(preorder[preIndex]);
preIndex++;
// find the index of first element of pre-order array
// in the in-order array.
int index = SearchValue(inorder,
preorder[preIndex - 1], s, e);
// Recursively create the left and right subtree.
root.left = BuildTreeRecur
(inorder, preorder, ref preIndex, s, index - 1);
root.right = BuildTreeRecur
(inorder, preorder, ref preIndex, index + 1, e);
return root;
}
static Node BuildTree(List<int> inorder,
List<int> preorder) {
int n = inorder.Count;
// Build the tree recursively.
int preIndex = 0;
return BuildTreeRecur(inorder, preorder,
ref preIndex, 0, n - 1);
}
static void PrintPostorder(Node root) {
if (root == null) return;
PrintPostorder(root.left);
PrintPostorder(root.right);
Console.Write(root.data + " ");
}
static void Main(string[] args) {
List<int> inorder = new List<int> { 3, 1, 4, 0, 5, 2 };
List<int> preorder = new List<int> { 0, 1, 3, 4, 2, 5 };
Node root = BuildTree(inorder, preorder);
PrintPostorder(root);
}
}Output
3 4 1 5 2 0
