Depth First Search (or DFS) for a graph resembles Depth First Traversal of a tree. Like trees, we move one by one all around our nearby vertices. We fully complete the traversal of all vertices reachable through that adjacent vertex when we walk across that vertex. We go to the next nearby vertex and resume the process after we have completed traversing one adjacent vertex and their reachable vertices. This is like a tree; we first go entirely over the left subtree then proceed to the right subtree. Graphs differ from trees primarily in that they may include cycles—a node may be visited more than once. We employ a boolean visited array to prevent repeatedly processing a node.
Example:
Input: adj = [[1, 2], [0, 2], [0, 1, 3, 4], [2], [2]]

Output: 1 2 0 3 4
Explanation: The source vertex s is 1. We visit it first, then we visit an adjacent. There are two adjacent 1, 0 and 2. We can pick any of the two (
Start at 1: Mark as visited. Output: 1
Move to 2: Mark as visited. Output: 2
Move to 0: Mark as visited. Output: 0 (backtrack to 2)
Move to 3: Mark as visited. Output: 3 (backtrack to 2)
Move to 4: Mark as visited. Output: 4 (backtrack to 1)
Input: [[2,3,1], [0], [0,4], [0], [2]]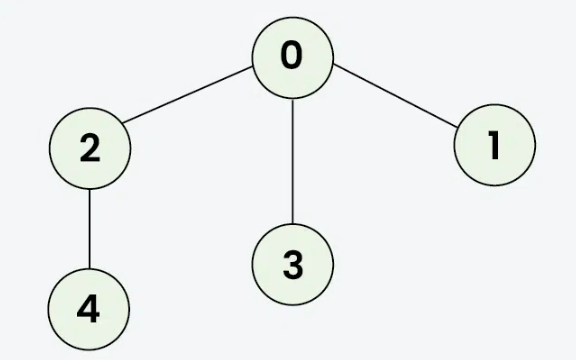
Output: 0 2 4 3 1
Explanation: DFS Steps:
Start at 0: Mark as visited. Output: 0
Move to 2: Mark as visited. Output: 2
Move to 4: Mark as visited. Output: 4 (backtrack to 2, then backtrack to 0)
Move to 3: Mark as visited. Output: 3 (backtrack to 0)
Move to 1: Mark as visited. Output: 1Starting from a given source, the algorithm searches all reachable vertices from the given source in a specified direction of undirectional graph. It resembles Preorder Tree Traversal in that we visit the root then recur for its offspring. A graph could have loops. We thus ensure that we do not treat a vertex once more by means of an additional visited array.
The fundamental knowledge of algorithms such Depth First Search or DFS is very important and also often asked in Technical exams and interview to have the strong knowledge of these concept you should check out our course Tech Interview 101 – From DSA to System Design in which you get the basic to advance knowledge of the data structure and algorithms.
Time complexity: O(V + E), in where V is the graph’s vertices count and E its edges count.
O(V + E) since an additional visited array of size V is needed, and stack size for recursive calls to DFSRec function.
Please find specifics in Complexity Analysis of Depth First Search.
DFS towards Complete Traversal of Disconnected Undirected Graph
In case of a disconnected graph, the above approach prints just those vertices that are reachable from the source, therefore depending on a source takes a source as an input. Let us now discuss the graph possibly disconnected and the method printing all vertices without any source.
The concept is straightforward: we call the above designed DFS for all instead of DFS for a single vertex.
Depth First Search or DFS on Directed Graph
One fundamental method for investigating graph structures is depth-first search (DFS). DFS in directed graphs can begin from a given point and search all the related nodes. It can also ensure that, even in cases of disconnected parts of the graph, every element in it is visited. Starting from a single point, this paper describes DFS’s operation and how one can traverse a complete graph including disconnected sections.
DFS from a Directed Graph’s Given Source
Starting at a given vertex and moving each node as far as we can go down in the path, Depth-First Search (DFS) from a given source explores a directed graph. We retreat to the previous vertex to investigate any other unexplored paths should we come upon a vertex devoid of unvisited neighbors. Finding pathways, verifying connectivity, and investigating all reachable nodes from a starting point are only three of the chores where this method is most helpful.
The Mechanism:
Maintain a boolean visited array to record which vertices have been seen already. When the graph has cycles, this will prevent one from running endlessly.
Visit all source node’s unvisited neighbors using recursion:
Initially marks the current vertex as visited and handles it (by printing its value, for instance).
Recursively then visits every unvisited neighbor of the current vertex.
Backtracks to the previous vertex to investigate other unvisited paths if a vertex lacks unvisited neighbors.
DFS for Disconnected Directed Graphs Complete Traversal
Edge directions in a directed graph allow us to go from one vertex to another just in the direction the edge points. One in which not all vertices are reachable from a single vertex is a disconnected graph.
In case of a disconnected graph, the above approach prints just those vertices that are reachable from the source, thereby depending on a source. Now let us discuss the graph maybe disconnected and the method that generates all vertices without any source.
We must make sure the DFS algorithm begins from every unvisited vertex in order to manage such a graph in DFS, therefore covering all components of the graph.
Time Complexity O(V + E). Here the temporal complexity is identical as we visit every vertex at most once and every edge is traversed twice in undirected and at most once (in directed).
Auxiliary Space: O(V + E), as an additional visited array of size V is needed, and stack size for recursive calls to DFSRec function.
