The shortest pathways between every pair of vertices in a given weighted directed graph can found by means of negative weights. For this issue, we have addressed Floyd Warshall Algorithm. The Floyd Warshall Algorithm boasts Θ(V3) as its time complexity.
We find all pair shortest paths in O(V2log V + VE) time using Johnson’s method. Using Dijkstra and Bellman-Ford as subroutines, Johnson’s method Considering every vertex as the source, applying Dijkstra’s Single Source shortest path algorithm for every vertex will yield all pair shortest paths in O(V*VLogV) time.
Although Dijkstra’s single-source shortest path appears to be a superior alternative than Floyd Warshall’s Algorithm (https://www.geeksforgeeks.org/floyd-warshall-algorithm-dp-16/?ref=lbp), the problem with Dijkstra’s approach is that it does not work for negative weight edge. Johnson’s method is to re-weight every edge and make them all positive, then run Dijkstra’s algorithm for every vertex.
How to convert a given graph into one with all non-negative weight edges?
One might consider a basic method of locating the least weight edge and applying this weight to every edge. Sadly, this doesn’t work since various pathways may have varying numbers of edges (See this for an example). Should there several routes from a vertex u to v, all paths must scaled by the same factor so that the shortest path stays the shortest in the modified graph. Every vertex will have a weight assigned using Johnson’s method. Assume h[u] to be the weight assigned to vertex u.
Reweight edges with vertex weights. The new weight, for an edge (u, v), for instance, becomes w(u, v) + h[u] – h[v]. The big advantage of this reweighting is that every set of pathways between any two vertices is raised by the same quantity and all negative weights turn non-negative. All h[] values of vertices on the path from s to t cancel each other; the weight of every path is raised by h[s] – h[t].
How are h[] values computed?
For this aim, Bellman-Ford algorithm is applied. The whole process follows here. Added to the graph, a new vertex links to every other vertex already present. h[] values define the shortest distances from the new vertex to every current vertex.
Method:
Allow G to be the specified graph. Create a new vertex s for the graph and link edges from that vertex to every vertex in G. Let G’s be the altered graph.
Run the Bellman-Ford method starting with s as the source on G’. Let Bellman-Ford’s computed distances be h[0], h[1],.. h[V-1]. Should we discover a negative weight cycle, then back off. As new vertex s lacks an edge, the negative weight cycle cannot be produced by it. From s, all edges are.
Reweight the original graph’s edges. Assign the new weight “original weight + h[u] – h[v],” for every edge (u, v).
Eliminate the extra vertex s and run Dijkstra’s method for every other vertex.
How does the transformation ensure nonnegative weight edges?
The following property is always true about h[] values as they are the shortest distances.
h[v] <= h[u] + w(u, v)
The property basically indicates that the shortest distance from s to v must be smaller than or equal to the shortest distance from s to u plus the weight of the edge (u, v). The revised weights are w(u, v) + h[u] – h[v]. The inequality “h[v] <= h[u] + w(u, v)” makes the value of the new weights either more than or equal to zero.
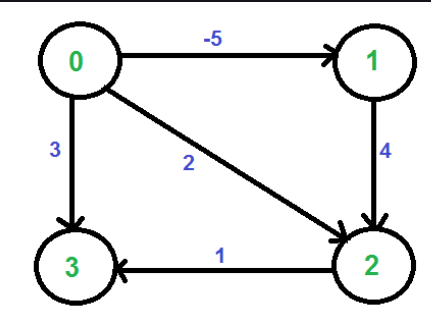
For instance, let us analyze the graph below.
We add edges from a source s to every vertex of the original graph. S is 4 in the next diagram.
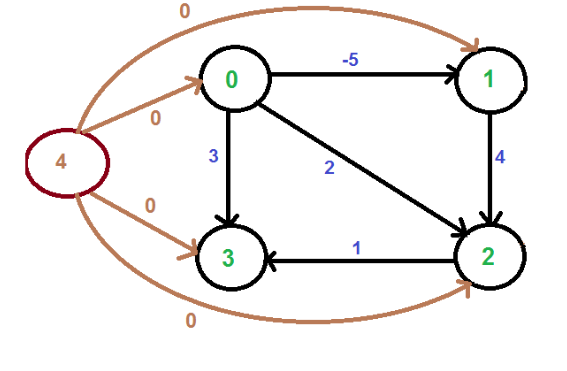
Bellman-Ford technique helps us to find the shortest distances from 4 to all other vertices. From 4 to 0, 1, 2, and 3 the shortest distances are 0, -5, -1, 0 accordingly, i.e., h[] = {0, -5, -1, 0}. After obtaining these distances, we eliminate the source vertex 4 and reweigh the edges by this algorithm. w(u, v) = u + h[u] – h[v].
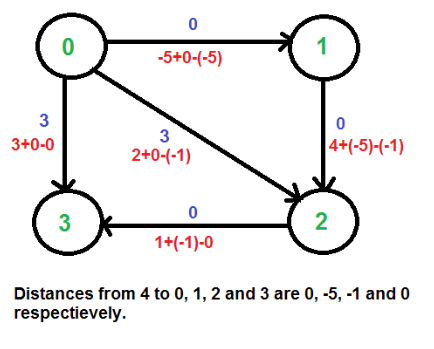
Now that all weights are positive, we may execute Dijkstra’s shortest path algorithm starting from every vertex.
Time Complexity: Bellman-Ford Algorithm once and Dijkstra termed V times constitute the primary steps in the method. Bellman Ford has O(VE) and Dijkstra has O(VLogV), time complexity. Time complexity is thus O(V2log V + VE) generally.
Johnson’s algorithm’s time complexity turns out to be Floyd Warshall’s Algorithm’s same.
