Topological sorting for directed acyclic graphs (DAG) is a linear ordering of vertices such that vertex u occurs before vertex v in the ordering for every directed edge u-v.
Note: Should a graph not be a DAG, topological sorting for that graph is not feasible.
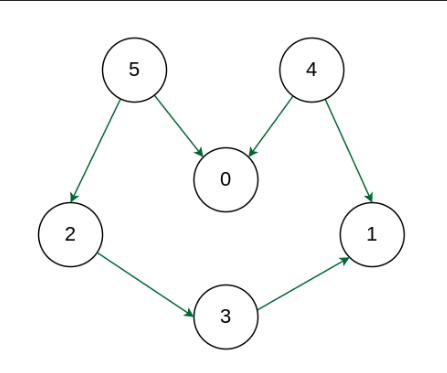
Output: 5 4 2 3 1 0
Explanation: The first vertex in topological sorting is always a vertex with an in-degree of 0 (a vertex with no incoming edges). A topological sorting of the following graph is “5 4 2 3 1 0”. There can be more than one topological sorting for a graph. Another topological sorting of the following graph is “4 5 2 3 1 0”. Depth First Traversal (DFS) prints a vertex and thereafter recursively calls DFS for its surrounding vertices. Before its nearby vertices in topological sorting, we must print a vertex.
For instance, unlike DFS, the vertex “4” should also printed before vertex “0,” even if the vertex “5” in the above graph should printed before vertex “0”. Topological sorting, thus, differs from DFS. For instance, although it is not a topological sorting, a DFS of the depicted graph is “5 2 3 1 0 4”.
Directed Acyclic Graphs’ (DAGs’) topological sorting
Before we can explain why Topological sort only exists for DAGs, let first address two questions: DAGs a unique type of graphs in which each edge directed so that no cycle exists in the graph. :
Why can graphs with undirected edges not have a topological sort?
This is thus because undirected edge between two vertices u and v denotes that an edge exists from u to v as well as from v to u. This means that both u and v depend on one other and none of them can show before the other in the topological ordering without generating a contradiction.
Why cannot Topological Sort be achieved for graphs with cycles?
Consider a graph with three vertices and edges {1 to 2, 2 to 3, 3 to 1} generating a cycle. Now it will always contradict our definition if we try to topologically arrange this graph beginning from any vertex. Topological sorting collapses when all the vertices in a cycle depend indirectly on each other.
Perhaps topological order is not unique.
A topological sorting is a dependency problem whereby the completion of one activity depends on the completion of multiple other tasks whose order can vary. Allow us to grasp this idea by means of an illustration:
Our assignment is to get to our school, thus first we must get ready. The dependency graph below shows the ones related to garments wearing. For instance you cannot wear shoes before donning socks.
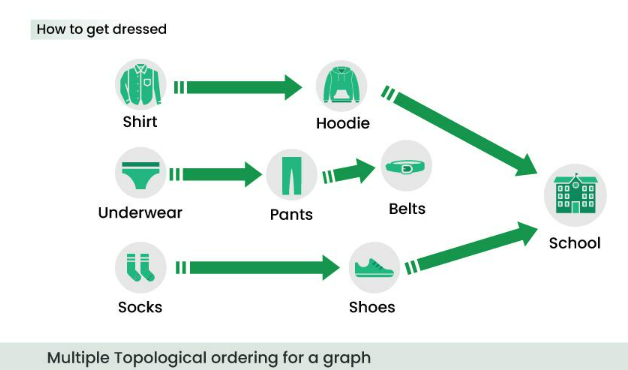
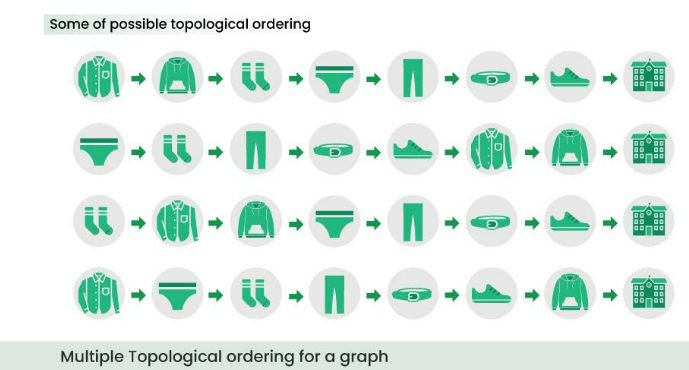
From the preceding picture, you would have already understood that there are several methods to get dressed; the below picture illustrates some of those ways.
Algorithm for DFS-based topological sorting:
Using Depth First Search (DFS), topological sorting is step-by-step explained here:
- Graph having n vertices and m-directed edges.
- Create an n-sized visited array and a stack initially.
- Treat every unvisited vertex in the graph as follows:
- Utilizing the vertex as the argument, call the DFS function.
- Mark the vertex as visited in the DFS function then recursively call it for every unvisited neighbor.
- Push the vertex onto the stack once every neighbor has seen her.
- Vertices have been visited, pop elements from the stack and add them to the output list until the stack runs empty.
- The final list is the graph’s topologically ordered sequence.
O(V+E) is time complexity. Above is just DFS with an additional stack. Time complexity thus is exactly DFS Auxiliary space: O(V). The stack needs the extra room.
Kahn’s Algorithm is the BFS based method used in topological sorting. The DFS based method covered above has temporal complexity; the Kahn’s approach has the same.
- Topological sort has the advantage of allowing one schedule jobs or events depending on interdependence.
- finds directed graph cycle patterns.
- effective for handling difficulties with priority restrictions.
- Topological Sort has disadvantages only relevant to directed acyclic graphs (DAGs), not fit for cyclic graphs.
- Perhaps not unique; several valid topological orders are possible.
Topological Sort’s applications
- Project management and work scheduling.
- In tools for software distribution such as Makefile.
- In systems of package management, dependence resolution.
- deciding the compilation sequence in systems of software development.
- Operating system deadlock detection
- Course plans for colleges.
- It is applied to determine shortest paths in weighted directed acyclic networks.
