Bridges in a graph- Data Structure and Algorithm

/ DSA Theory / By
Spread the love

The work is to identify the Bridges in an undirected graph.

In an undirected linked graph, an edge is a bridge if removing it separates the graph. The definition is same for a disconnected undirected graph: a bridge is an edge removal that generates more disconnected components.

Bridges, like articulation points, expose weaknesses in a linked network and help to create dependable networks.


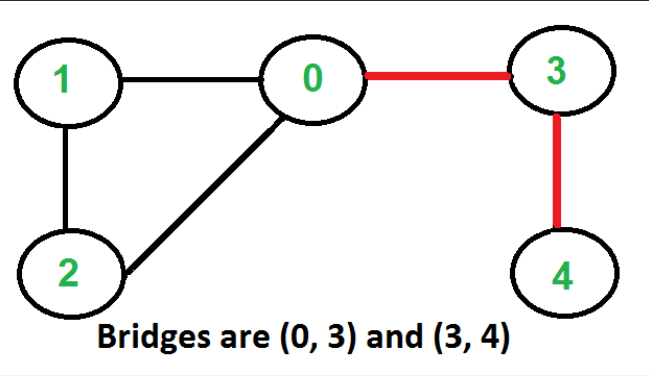
Output: (0, 3) and (3, 4)

Input:

Output: (1, 6)

Input:

Output: (0, 1), (1, 2), and (2, 3)

Here is a naive approach to address the issue:

Eliminate all edges one by one and observe whether the removal of one produces a disconnected graph.

Use the guidelines below to carry out the concept:

  • Apply the following for every edge (u, v):
  • Get (u, v) off the graph.
  • Check whether the graph stays connected—using BFS or DFS—here.
  • Reversal of (u, v) back to the graph.
  • Time Complexity: O(E*(V+E)) for a graph expressed as an adjacency list.
  • Auxiliary Space: O(V+E)

Find bridges in a graph applying Tarjan’s Algorithm.


Before turning toward the approach, find out which edge is known as a bridge. Assume there is an edge from u -> v; now, should v not be reachable from any other edge, u -> v edge becomes bridge. Our method is based on intuition; so, take some time to grab it.

Algorithm: –

We require certain data structures to apply this method:

visited[ ] = to monitor the visited vertices for DFS implementation disc[ ] = to keep track when for the first time that specific vertex is reached low[ ] = to keep track of the lowest feasible time by which we can reach that vertex “other than parent,” so enabling the particular node to be reached other than parent should the parent edge be deleted.
We will travel the graph using DFS traversal but with minor changes i.e., while traversing we will keep track of the parent node by which the particular node is reached since we will update the low[node] = min(low[all it’s adjacent node except parent]). thus we need to keep track of the parent.

While moving nearby nodes allow “v” of a given node let “u,” then three scenarios develop.

  1. v is parent of u then,

Skip that iteration.

  1. v goes then as well.

Change the low of u by means of low[u] = min( low[u], disc[v]) This results when a node can be visited by more than one node; low is to monitor the lowest feasible time thus we will update it.

  1. v does not visit then either.

As we know v cannot be parent; so, we have addressed that scenario first. Call the DFS to traverse forward now update the low[u] = min( low[u], low[v].
The edge u -> v is a bridge since the lowest possible to time to reach “v” is more than “u” hence we cannot reach “v” without “u”.

Time Complexity: O(V+E), 

  • The above approach uses simple DFS along with Tarjan’s Algorithm. 
  • So time complexity is the same as DFS which is O(V+E) for adjacency list representation of the graph.

Auxiliary Space: O(V) used for visited, disc and low arrays.