Check Sudoku board configuration is valid or not

Using Array of Fixed Length

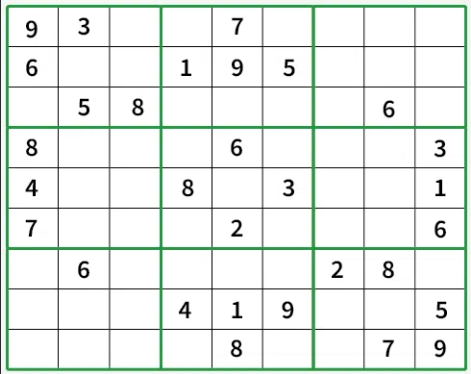
We can track each number in rows, columns, and sub-matrix using auxiliary arrays rather than any hash table to record seen/visited elements. Arrays allow us to remove the hash overhead.

Methodically approaching:

• We track which integers have already appeared in each row, column, and sub-matrix accordingly using three 2D arrays (rows, cols, subMat).
• We skip each cell whether it is 0 (empty). Otherwise, we search the relevant row, column, or sub-matrix for the number’s past presence. Indeed, the matrix is invalid.
• Calculated as (i / 3) * 3 + j / 3, the sub-matrix index considers both row and column indices.
• Marked as seen/visited if the current number is not visited prior in the current row, column, or sub-matrix.

C++

#include <bits/stdc++.h>
using namespace std;

// Function to check if the Sudoku matrix is valid
int isValid(vector<vector<int>> & mat){
  
    // Track of numbers in rows, columns, and sub-matrix
    vector<vector<int>> rows(10, vector<int>(10, 0));
    vector<vector<int>> cols(10, vector<int>(10, 0));
    vector<vector<int>> subMat(10, vector<int>(10, 0));

    for (int i = 0; i < 9; i++){
        for (int j = 0; j < 9; j++){

            // Skip empty cells
            if (mat[i][j] == 0)
                continue;

            // Current value
            int val = mat[i][j]; 

            // Check for duplicates in row
            if (rows[i][val] == 1)
                return false;

            // Mark as seen
            rows[i][val] = 1; 

            // Check for duplicates in column
            if (cols[j][val] == 1)
                return false;

            // Mark as seen
            cols[j][val] = 1; 

            // Check for duplicates in sub-grid
            int idx = (i / 3) * 3 + j / 3;
            if (subMat[idx][val] == 1)
                return false;

            // Mark as seen
            subMat[idx][val] = 1; 
        }
    }

    return true;
}

int main(){
    vector<vector<int>> mat = {
        {5, 3, 0, 0, 7, 0, 0, 0, 0},
        {6, 0, 0, 1, 9, 5, 0, 0, 0},
        {0, 9, 8, 0, 0, 0, 0, 6, 0},
        {8, 0, 0, 0, 6, 0, 0, 0, 3},
        {4, 0, 0, 8, 0, 3, 0, 0, 1},
        {7, 0, 0, 0, 2, 0, 0, 0, 6},
        {0, 6, 0, 0, 0, 0, 2, 8, 0},
        {0, 0, 0, 4, 1, 9, 0, 0, 5},
        {0, 0, 0, 0, 8, 0, 0, 7, 9}};

    cout << (isValid(mat) ? "true" : "false") << "\n";

    return 0;
}

C

#include <stdio.h>
#include <stdbool.h>

int isValid(int mat[9][9]) {
  
    // Track of numbers in rows, columns, and sub-matrix
    int rows[10][10] = {0};
    int cols[10][10] = {0};
    int subMat[10][10] = {0};

    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
          
            // Skip empty cells
            if (mat[i][j] == 0)
                continue;

            // Current value
            int val = mat[i][j];

            // Check for duplicates in row
            if (rows[i][val] == 1)
                return false; // false

            // Mark as seen
            rows[i][val] = 1;

            // Check for duplicates in column
            if (cols[j][val] == 1)
                return false; // false

            // Mark as seen
            cols[j][val] = 1;

            // Check for duplicates in sub-grid
            int idx = (i / 3) * 3 + j / 3;
            if (subMat[idx][val] == 1)
                return 0; 

            // Mark as seen
            subMat[idx][val] = 1;
        }
    }

    return true;
}

int main() {
    int mat[9][9] = {
        {5, 3, 0, 0, 7, 0, 0, 0, 0},
        {6, 0, 0, 1, 9, 5, 0, 0, 0},
        {0, 9, 8, 0, 0, 0, 0, 6, 0},
        {8, 0, 0, 0, 6, 0, 0, 0, 3},
        {4, 0, 0, 8, 0, 3, 0, 0, 1},
        {7, 0, 0, 0, 2, 0, 0, 0, 6},
        {0, 6, 0, 0, 0, 0, 2, 8, 0},
        {0, 0, 0, 4, 1, 9, 0, 0, 5},
        {0, 0, 0, 0, 8, 0, 0, 7, 9}
    };

    printf("%s\n", isValid(mat) ? "true" : "false");

    return 0;
}

Java

class GfG {
    static boolean isValid(int[][] mat){

        // Track of numbers in rows, columns,
        // and sub-matrix
        int[][] rows = new int[10][10];
        int[][] cols = new int[10][10];
        int[][] subMat = new int[10][10];

        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {

                // Skip empty cells
                if (mat[i][j] == 0)
                    continue;

                // Current value
                int val = mat[i][j];

                // Check for duplicates in row
                if (rows[i][val] == 1)
                    return false;

                // Mark as seen
                rows[i][val] = 1;

                // Check for duplicates in column
                if (cols[j][val] == 1)
                    return false;

                // Mark as seen
                cols[j][val] = 1;

                // Check for duplicates in sub-grid
                int idx = (i / 3) * 3 + j / 3;
                if (subMat[idx][val] == 1)
                    return false;

                // Mark as seen
                subMat[idx][val] = 1;
            }
        }
        return true;
    }

    public static void main(String[] args)
    {
        int[][] mat = { { 5, 3, 0, 0, 7, 0, 0, 0, 0 },
                        { 6, 0, 0, 1, 9, 5, 0, 0, 0 },
                        { 0, 9, 8, 0, 0, 0, 0, 6, 0 },
                        { 8, 0, 0, 0, 6, 0, 0, 0, 3 },
                        { 4, 0, 0, 8, 0, 3, 0, 0, 1 },
                        { 7, 0, 0, 0, 2, 0, 0, 0, 6 },
                        { 0, 6, 0, 0, 0, 0, 2, 8, 0 },
                        { 0, 0, 0, 4, 1, 9, 0, 0, 5 },
                        { 0, 0, 0, 0, 8, 0, 0, 7, 9 } };

        System.out.println(isValid(mat) ? "true" : "false");
    }
}

Python

def isValid(mat):
    # Track of numbers in rows, columns, and sub-matrix
    rows = [[0] * 10 for _ in range(10)]
    cols = [[0] * 10 for _ in range(10)]
    subMat = [[0] * 10 for _ in range(10)]

    for i in range(9):
        for j in range(9):
            # Skip empty cells
            if mat[i][j] == 0:
                continue

            # Current value
            val = mat[i][j]

            # Check for duplicates in row
            if rows[i][val] == 1:
                return False

            # Mark as seen
            rows[i][val] = 1

            # Check for duplicates in column
            if cols[j][val] == 1:
                return False

            # Mark as seen
            cols[j][val] = 1

            # Check for duplicates in sub-grid
            idx = (i // 3) * 3 + j // 3
            if subMat[idx][val] == 1:
                return False

            # Mark as seen
            subMat[idx][val] = 1

    return True


mat = [
    [5, 3, 0, 0, 7, 0, 0, 0, 0],
    [6, 0, 0, 1, 9, 5, 0, 0, 0],
    [0, 9, 8, 0, 0, 0, 0, 6, 0],
    [8, 0, 0, 0, 6, 0, 0, 0, 3],
    [4, 0, 0, 8, 0, 3, 0, 0, 1],
    [7, 0, 0, 0, 2, 0, 0, 0, 6],
    [0, 6, 0, 0, 0, 0, 2, 8, 0],
    [0, 0, 0, 4, 1, 9, 0, 0, 5],
    [0, 0, 0, 0, 8, 0, 0, 7, 9]
]

print("true" if isValid(mat) else "false")

C#

using System;

class GfG {
  
    // Function to check if the Sudoku matrix is valid
    static bool IsValid(int[, ] mat){
      
        // Track of numbers in rows, columns, and sub-matrix
        int[, ] rows = new int[10, 10];
        int[, ] cols = new int[10, 10];
        int[, ] subMat = new int[10, 10];

        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                // Skip empty cells
                if (mat[i, j] == 0)
                    continue;

                // Current value
                int val = mat[i, j];

                // Check for duplicates in row
                if (rows[i, val] == 1)
                    return false;

                // Mark as seen
                rows[i, val] = 1;

                // Check for duplicates in column
                if (cols[j, val] == 1)
                    return false;

                // Mark as seen
                cols[j, val] = 1;

                // Check for duplicates in sub-grid
                int idx = (i / 3) * 3 + j / 3;
                if (subMat[idx, val] == 1)
                    return false;

                // Mark as seen
                subMat[idx, val] = 1;
            }
        }

        return true;
    }

    static void Main(){
        int[, ] mat = { { 5, 3, 0, 0, 7, 0, 0, 0, 0 },
                        { 6, 0, 0, 1, 9, 5, 0, 0, 0 },
                        { 0, 9, 8, 0, 0, 0, 0, 6, 0 },
                        { 8, 0, 0, 0, 6, 0, 0, 0, 3 },
                        { 4, 0, 0, 8, 0, 3, 0, 0, 1 },
                        { 7, 0, 0, 0, 2, 0, 0, 0, 6 },
                        { 0, 6, 0, 0, 0, 0, 2, 8, 0 },
                        { 0, 0, 0, 4, 1, 9, 0, 0, 5 },
                        { 0, 0, 0, 0, 8, 0, 0, 7, 9 } };

        Console.WriteLine(IsValid(mat) ? "true" : "false");
    }
}

Time complexity O(n^2), where n = Sudoku matrix size—that is, 9. This is so as we go across all nn matrix cells iteratively. O(n^2) auxiliary space resulting from three 2D arrays of size nn rows, cols, subMatrix.