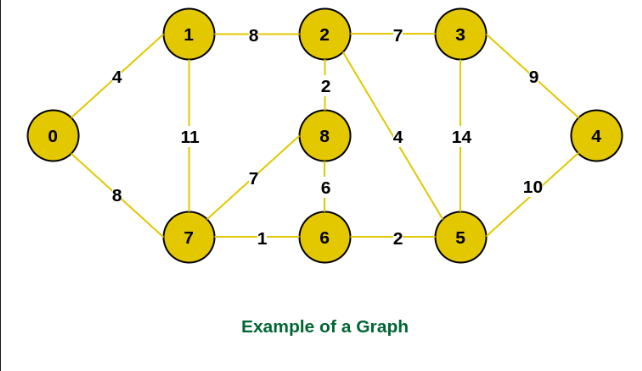
Fundamental in nature, minimum spanning trees (MST) find use in network design, clustering, and optimization challenges in graph theory. Prim’s and Kruskal’s algorithms among the two most often used ones for determining the MST of a graph. Though they accomplish the same objective, both techniques do it in rather distinct ways. The variations between them will be discussed in this paper. To enable the selection of the appropriate method for particular kinds of graphs and uses.
Designed as a greedy method, Prim’s Algorithm gradually generates the MST. Starting with a single vertex, it develops the MST one edge at a time always selecting the smallest edge that links a vertex in the MST to a vertex outside the MST.
Steps of Prim’s Algorithm:
- Initialism: Mark any arbitrary vertex you start with as part of the MST.
- From the collection of edges linking vertices in the MST to those outside the MST, choose the edge with the lowest weight.
- Update: Add the MST the chosen edge and the linked vertex.
- Until all vertices covered in the MST, keep repeating the edge choosing and updating processes.
- Usually employing a priority queue, Prim’s algorithm effectively chooses the smallest weight edge at every stage.
Though it does things differently, Kruskal’s Algorithm is likewise a greedy one. Starting with all the vertices and no edges, it adds edges one by one in increasing order of weight to ensure no cycles develop until the MST is complete.
Algorithm Kruskal’s steps:
- Sort every graph edge according to weight in non-decreasing sequence at first.
- Beginning from the smallest edge, add the edge to the MST if it does not form a cycle with the currently included edges.
- Detect and stop cycles by means of a union-find data structure.
- Continuum: Till the MST has exactly (V-1) edges, where V is the number of vertices, keep adding edges.
- Main Variations Between Prim’s and Kruskal’s Algorithm for MST
The main variations between Prim’s and Kruskal’s methods for minimum spanning tree (MST) discovery are compiled here:
| Feature | PrimŌĆÖs Algorithm | KruskalŌĆÖs Algorithm |
|---|---|---|
| Approach | Vertex-based, grows the MST one vertex at a time | Edge-based, adds edges in increasing order of weight |
| Data Structure | Priority queue (min-heap) | Union-Find data structure |
| Graph Representation | Adjacency matrix or adjacency list | Edge list |
| Initialization | Starts from an arbitrary vertex | Starts with all vertices as separate trees (forest) |
| Edge Selection | Chooses the minimum weight edge from the connected vertices | Chooses the minimum weight edge from all edges |
| Cycle Management | Not explicitly managed; grows connected component | Uses Union-Find to avoid cycles |
| Complexity | O(V^2) for adjacency matrix, O((E + V) log V) with a priority queue | O(E log E) or O(E log V), due to edge sorting |
| Suitable for | Dense graphs | Sparse graphs |
| Implementation Complexity | Relatively simpler in dense graphs | More complex due to cycle management |
| Parallelism | Difficult to parallelize | Easier to parallelize edge sorting and union operations |
| Memory Usage | More memory for priority queue | Less memory if edges can be sorted externally |
| Example Use Cases | Network design, clustering with dense connections | Road networks, telecommunications with sparse connections |
| Starting Point | Requires a starting vertex | No specific starting point, operates on global edges |
| Optimal for | Dense graphs where adjacency list is used | Sparse graphs where edge list is efficient |
Conclusion
PrimŌĆÖs┬Āand┬ĀKruskalŌĆÖs┬Āalgorithms are both powerful tools for finding the┬ĀMST┬Āof a graph, each with its unique advantages.┬ĀPrimŌĆÖs algorithm┬Ātypically preferred for dense graphs, leveraging its efficient priority queue-based approach, while┬ĀKruskalŌĆÖs algorithm┬Āexcels in handling sparse graphs with its edge-sorting and union-find techniques. Understanding the structural differences and appropriate use cases for each algorithm ensures optimal performance in various graph-related problems.
