Given a list indicating words and two separate words, startWord and targetWorda list of distinct words with comparable lengths. Determine which transformation sequences from startWord to targetWord are the shortest. They can be returned in any feasible order.
The following requirements must be considered in this problem statement:
- Only lowercase characters may be used in a word.
- Each transformation can only alter one letter.
- Every altered word, including the targetWord, needs to be present in the wordList.
- The wordList may or may not contain startWord.
- If such a transformation sequence does not exist, return an empty list.
Examples:
Example 1:
Input:
startWord = "der", targetWord = "dfs",
wordList = {"des","der","dfr","dgt","dfs"}
Output:
[ [ “der”, “dfr”, “dfs” ], [ “der”, “des”, “dfs”] ]
Explanation:
The length of the smallest transformation sequence here is 3.
Following are the only two shortest ways to get to the targetWord from the startWord :
"der" -> ( replace ‘r’ by ‘s’ ) -> "des" -> ( replace ‘e’ by ‘f’ ) -> "dfs".
"der" -> ( replace ‘e’ by ‘f’ ) -> "dfr" -> ( replace ‘r’ by ‘s’ ) -> "dfs".
Example 2:
Input:
startWord = "gedk", targetWord= "geek"
wordList = {"geek", "gefk"}
Output:
[ [ “gedk”, “geek” ] ]
Explanation:
The length of the smallest transformation sequence here is 2.
Following is the only shortest way to get to the targetWord from the startWord :
"gedk" -> ( replace ‘d’ by ‘e’ ) -> "geek".
Intuition: The idea behind applying the BFS traversal strategy to these types of issues is that, if we pay close attention, we continue to replace the characters one by one, giving the impression that we are going level-wise to get to the targetWord. It is evident from the example below that there are two ways to get to the targetWord.
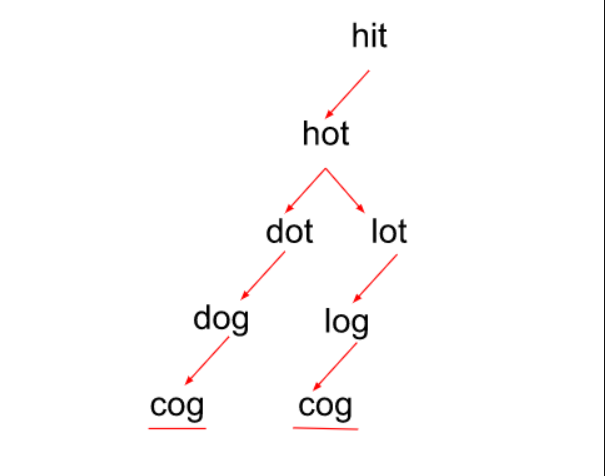
Since we require all of the shortest sequences to get to the destination word, unlike the prior case, we continue the traversal for as many instances of the targetWord as possible rather than stopping it at the first occurrence. The only difficulty here is that, even if a word matches the changed word during character replacement, we do not have to remove it from the wordList right away. Rather, we remove it whenever the traversal for a specific level is over, enabling us to investigate every potential route. This enables us to find several sequences using related words that lead to the targetWord.
We can infer from the preceding image that there are two shortest feasible sequences that lead to the word “cog.”
C++
#include <bits/stdc++.h>
using namespace std;
class Solution
{
public:
vector<vector<string>> findSequences(string beginWord, string endWord,
vector<string> &wordList)
{
// Push all values of wordList into a set
// to make deletion from it easier and in less time complexity.
unordered_set<string> st(wordList.begin(), wordList.end());
// Creating a queue ds which stores the words in a sequence which is
// required to reach the targetWord after successive transformations.
queue<vector<string>> q;
// BFS traversal with pushing the new formed sequence in queue
// when after a transformation, a word is found in wordList.
q.push({beginWord});
// A vector defined to store the words being currently used
// on a level during BFS.
vector<string> usedOnLevel;
usedOnLevel.push_back(beginWord);
int level = 0;
// A vector to store the resultant transformation sequence.
vector<vector<string>> ans;
while (!q.empty())
{
vector<string> vec = q.front();
q.pop();
// Now, erase all words that have been
// used in the previous levels to transform
if (vec.size() > level)
{
level++;
for (auto it : usedOnLevel)
{
st.erase(it);
}
}
string word = vec.back();
// store the answers if the end word matches with targetWord.
if (word == endWord)
{
// the first sequence where we reached end
if (ans.size() == 0)
{
ans.push_back(vec);
}
else if (ans[0].size() == vec.size())
{
ans.push_back(vec);
}
}
for (int i = 0; i < word.size(); i++)
{
// Now, replace each character of ‘word’ with char
// from a-z then check if ‘word’ exists in wordList.
char original = word[i];
for (char c = 'a'; c <= 'z'; c++)
{
word[i] = c;
if (st.count(word) > 0)
{
// Check if the word is present in the wordList and
// push the word along with the new sequence in the queue.
vec.push_back(word);
q.push(vec);
// mark as visited on the level
usedOnLevel.push_back(word);
vec.pop_back();
}
}
word[i] = original;
}
}
return ans;
}
};
// A comparator function to sort the answer.
bool comp(vector<string> a, vector<string> b)
{
string x = "", y = "";
for (string i : a)
x += i;
for (string i : b)
y += i;
return x < y;
}
int main()
{
vector<string> wordList = {"des", "der", "dfr", "dgt", "dfs"};
string startWord = "der", targetWord = "dfs";
Solution obj;
vector<vector<string>> ans = obj.findSequences(startWord, targetWord, wordList);
// If no transformation sequence is possible.
if (ans.size() == 0)
cout << -1 << endl;
else
{
sort(ans.begin(), ans.end(), comp);
for (int i = 0; i < ans.size(); i++)
{
for (int j = 0; j < ans[i].size(); j++)
{
cout << ans[i][j] << " ";
}
cout << endl;
}
}
return 0;
}Java
import java.util.*;
import java.lang.*;
import java.io.*;
// A comparator function to sort the answer.
class comp implements Comparator < ArrayList < String >> {
public int compare(ArrayList < String > a, ArrayList < String > b) {
String x = "";
String y = "";
for (int i = 0; i < a.size(); i++)
x += a.get(i);
for (int i = 0; i < b.size(); i++)
y += b.get(i);
return x.compareTo(y);
}
}
public class Main {
public static void main(String[] args) throws IOException {
String startWord = "der", targetWord = "dfs";
String[] wordList = {
"des",
"der",
"dfr",
"dgt",
"dfs"
};
Solution obj = new Solution();
ArrayList < ArrayList < String >> ans = obj.findSequences(startWord, targetWord, wordList);
// If no transformation sequence is possible.
if (ans.size() == 0)
System.out.println(-1);
else {
Collections.sort(ans, new comp());
for (int i = 0; i < ans.size(); i++) {
for (int j = 0; j < ans.get(i).size(); j++) {
System.out.print(ans.get(i).get(j) + " ");
}
System.out.println();
}
}
}
}
class Solution {
public ArrayList < ArrayList < String >> findSequences(String startWord, String targetWord,
String[] wordList) {
// Push all values of wordList into a set
// to make deletion from it easier and in less time complexity.
Set < String > st = new HashSet < String > ();
int len = wordList.length;
for (int i = 0; i < len; i++) {
st.add(wordList[i]);
}
// Creating a queue ds which stores the words in a sequence which is
// required to reach the targetWord after successive transformations.
Queue < ArrayList < String >> q = new LinkedList < > ();
ArrayList < String > ls = new ArrayList < > ();
ls.add(startWord);
q.add(ls);
ArrayList < String > usedOnLevel = new ArrayList < > ();
usedOnLevel.add(startWord);
int level = 0;
// A vector to store the resultant transformation sequence.
ArrayList < ArrayList < String >> ans = new ArrayList < > ();
int cnt = 0;
// BFS traversal with pushing the new formed sequence in queue
// when after a transformation, a word is found in wordList.
while (!q.isEmpty()) {
cnt++;
ArrayList < String > vec = q.peek();
q.remove();
// Now, erase all words that have been
// used in the previous levels to transform
if (vec.size() > level) {
level++;
for (String it: usedOnLevel) {
st.remove(it);
}
}
String word = vec.get(vec.size() - 1);
// store the answers if the end word matches with targetWord.
if (word.equals(targetWord)) {
// the first sequence where we reached the end.
if (ans.size() == 0) {
ans.add(vec);
} else if (ans.get(0).size() == vec.size()) {
ans.add(vec);
}
}
for (int i = 0; i < word.length(); i++) {
// Now, replace each character of ‘word’ with char
// from a-z then check if ‘word’ exists in wordList.
for (char c = 'a'; c <= 'z'; c++) {
char replacedCharArray[] = word.toCharArray();
replacedCharArray[i] = c;
String replacedWord = new String(replacedCharArray);
if (st.contains(replacedWord) == true) {
vec.add(replacedWord);
// Java works by reference, so enter the copy of vec
// otherwise if you remove word from vec in next lines, it will
// remove from everywhere
ArrayList < String > temp = new ArrayList < > (vec);
q.add(temp);
// mark as visited on the level
usedOnLevel.add(replacedWord);
vec.remove(vec.size() - 1);
}
}
}
}
return ans;
}
}Output:
der des dfs
der dfr dfs
