Find the shortest paths from the source to every other vertex in the provided graph with a weighted graph and a source vertex in the graph.
Note: There isn’t any negative edge on the shown graph.
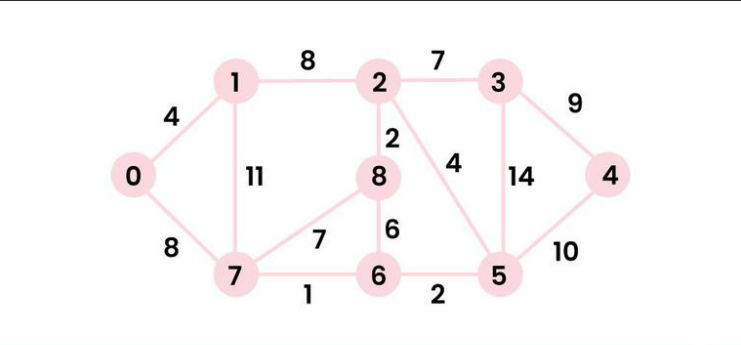
Input: src = 0, the graph is shown below.
Output: 0 4 12 19 21 11 9 8 14
Explanation: The distance from 0 to 1 = 4.
The minimum distance from 0 to 2 = 12. 0->1->2
The minimum distance from 0 to 3 = 19. 0->1->2->3
The minimum distance from 0 to 4 = 21. 0->7->6->5->4
The minimum distance from 0 to 5 = 11. 0->7->6->5
The minimum distance from 0 to 6 = 9. 0->7->6
The minimum distance from 0 to 7 = 8. 0->7
The minimum distance from 0 to 8 = 14. 0->1->2->8 Dijkstra’s Algorithm using Adjacency Matrix :
Generating a shortest path tree (SPT) using a specified source as a root is the goal. Keep a two-set Adjacency Matrix maintained.
One set comprises vertices covered by the shortest-path tree; another set comprises vertices not yet included in that tree.
Discover a vertex in the other set (set not yet included) with a minimum distance from the source at every stage of the method.
Method:
- Track vertices included in the shortest path tree, i.e., whose minimal distance from the source is computed and finalized, by use of a set sptSet (shortest path tree set.). This set starts off empty.
- Give every verticle in the input graph a distance value. Start all distances as INFINITE. Set the distance value for the source vertex to 0 so it is chosen first.
- Even if sptSet excludes all vertices
- Choose a vertex u with a minimum distance value not found in sptSet.
- Add u to spptSet.
- Update then the distance value of every adjacent vertex of u.
- Go over all nearby vertices iteratively to update the distance values.
- Update the distance value of each neighboring vertex v if the total of the weight of edge u-v and u’s distance value from the source is less than v’s distance value.
- Note: The set of vertices contained in SPT is shown by a boolean array sptSet[]. Should a value sptSet[v] be true, vertex v is incorporated in SPT; otherwise, not. All vertices’ shortest distance values are kept in array dist[].
Notes:
Though it computes the shortest distance, the code does not compute the path information. Create a parent array, update it when distance changed, then display the shortest path from source to several vertices from that parent array.
The period The complexity of the application is O(V 2 ). Using a binary heap will assist one to decrease the input graph represented using adjacency list to O(E * log V). For further information, kindly consult Dijkstra’s Algorithm for Adjacent List Representation.
Graphs having negative weight cycles cannot benefit from Dijkstra’s algorithm.
Why Dijkstra’s Algorithms fails for the Graphs with negative edges?
Negative weights problematic since Dijkstra’s algorithm supposes that once a node included to the list of visited nodes, its distance completed and will not vary. Negative weights, however, can cause this assumption to produce erroneous findings.
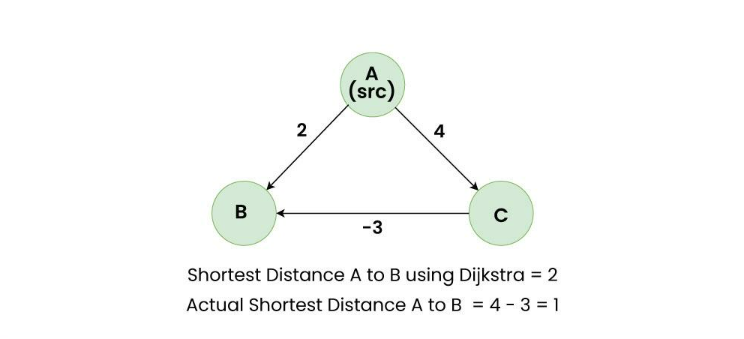
A is the source node in the above graph; among the edges A to B and A to C, A to B has the smaller weight and Dijkstra assigns the shortest distance of B as 2; yet, because of existence of a negative edge from C to B, the actual shortest distance reduces to 1 which Dijkstra misses to discover.
Dijkstra’s Algorithm using Adjacency List in O(E logV):
Heap (or priority queue) always advised to be used for Dijkstra’s method since the necessary actions (extract minimum and decrease key) fit with the speciality of the heap (or priority queue). The issue is, though, that priority_queue does not handle the decreasing key. Instead of updating a key to fix this, enter one additional duplicate of it. We thus let the priority queue to contain several instances of the same vertex. This method has below main characteristics and does not call for reducing important processes.
We add one more instance of a vertex in priority_queue if the distance of a vertex decreases. We just examine the instance with least distance and overlook other instances even in cases of several occurrences.
O(logE) is the same as O(logV) hence the time complexity stays O(E * LogV). At most O(E) vertices will be in the priority queue.
O(E * logV) where E is the number of edges and V is the number of vertices determines time complexity.
O(V) auxiliary space
Google maps shows shortest distance between source and destination by means of Dijkstra’s Algorithm.
Dijkstra’s technique lays the foundation for several routing systems like OSPF (Open Shortest Path First) and IS-IS (Intermediate System to Intermediate System) in computer networking.
The Dijkstra’s algorithm applied in traffic management systems and transportation to maximize traffic flow, reduce congestion, and create the most effective vehicle routes.
Dijkstra’s method helps airlines create fly routes that cut travel time and fuel use.
Electronic design automation uses Dijkstra’s algorithm to route connections on very-large-scale integration (VLSI) chips and integrated circuits.
