Determine the biggest rectangular area a given histogram can have where a number of adjacent bars allow the biggest rectangle to be formed. Assume for simplicity that the width of all bars is one unit.
Take the following histogram with 7 bars of heights {6, 2, 5, 4, 5, 1, 6} for instance. Twelve is the largest rectangle that may be formed; the max area rectangle is underlined in red below.
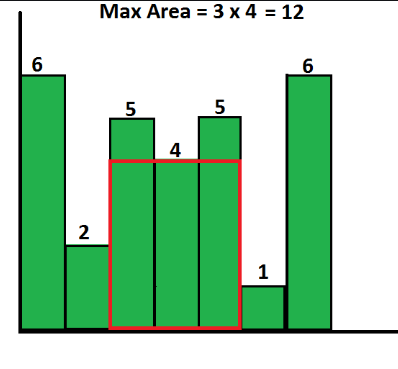
One may find a straightforward solution by first considering all bars as points of reference and then computing the area of every rectangle beginning with each bar. At last return maximum of all conceivable areas. O(n^2) would be the time complexity of this solution.
Solving this in O(nLogn) time will require Divide and Conquer. Finding the least value in the given array is the aim. The maximum area follows three values once we have index of the minimum value.
- Maximum area on the left side of the minimal value—not including the min value
- Maximum area in the right side of minimal value (without including the min value)
- Minum value times number of bars.
- Recursively one can determine the areas left and right of minimal value bar. Should we seek the smallest value using linear search, the worst case time complexity of this method changes to O(n^2). In worst case, we always have (n-1) elements in one side and 0 elements in other side and if the finding minimum takes O(n) time, we get the recurrence comparable to worst case of Quick Sort.
- How effectively can one determine the minimum? For this one can apply range minimum query utilizing segment tree. We construct segment tree based on the specified histogram heights. All range minimum searches in a segment tree take O(Logn) time once it is constructed. Thus, the overall complexity of the algorithm gets.
C++
// A Divide and Conquer Program to find maximum rectangular area in a histogram
#include <bits/stdc++.h>
using namespace std;
// A utility function to find minimum of three integers
int max(int x, int y, int z)
{ return max(max(x, y), z); }
// A utility function to get minimum of two numbers in hist[]
int minVal(int *hist, int i, int j)
{
if (i == -1) return j;
if (j == -1) return i;
return (hist[i] < hist[j])? i : j;
}
// A utility function to get the middle index from corner indexes.
int getMid(int s, int e)
{ return s + (e -s)/2; }
/* A recursive function to get the index of minimum value in a given range of
indexes. The following are parameters for this function.
hist --> Input array for which segment tree is built
st --> Pointer to segment tree
index --> Index of current node in the segment tree. Initially 0 is
passed as root is always at index 0
ss & se --> Starting and ending indexes of the segment represented by
current node, i.e., st[index]
qs & qe --> Starting and ending indexes of query range */
int RMQUtil(int *hist, int *st, int ss, int se, int qs, int qe, int index)
{
// If segment of this node is a part of given range, then return the
// min of the segment
if (qs <= ss && qe >= se)
return st[index];
// If segment of this node is outside the given range
if (se < qs || ss > qe)
return -1;
// If a part of this segment overlaps with the given range
int mid = getMid(ss, se);
return minVal(hist, RMQUtil(hist, st, ss, mid, qs, qe, 2*index+1),
RMQUtil(hist, st, mid+1, se, qs, qe, 2*index+2));
}
// Return index of minimum element in range from index qs (query start) to
// qe (query end). It mainly uses RMQUtil()
int RMQ(int *hist, int *st, int n, int qs, int qe)
{
// Check for erroneous input values
if (qs < 0 || qe > n-1 || qs > qe)
{
cout << "Invalid Input";
return -1;
}
return RMQUtil(hist, st, 0, n-1, qs, qe, 0);
}
// A recursive function that constructs Segment Tree for hist[ss..se].
// si is index of current node in segment tree st
int constructSTUtil(int hist[], int ss, int se, int *st, int si)
{
// If there is one element in array, store it in current node of
// segment tree and return
if (ss == se)
return (st[si] = ss);
// If there are more than one elements, then recur for left and
// right subtrees and store the minimum of two values in this node
int mid = getMid(ss, se);
st[si] = minVal(hist, constructSTUtil(hist, ss, mid, st, si*2+1),
constructSTUtil(hist, mid+1, se, st, si*2+2));
return st[si];
}
/* Function to construct segment tree from given array. This function
allocates memory for segment tree and calls constructSTUtil() to
fill the allocated memory */
int *constructST(int hist[], int n)
{
// Allocate memory for segment tree
int x = (int)(ceil(log2(n))); //Height of segment tree
int max_size = 2*(int)pow(2, x) - 1; //Maximum size of segment tree
int *st = new int[max_size];
// Fill the allocated memory st
constructSTUtil(hist, 0, n-1, st, 0);
// Return the constructed segment tree
return st;
}
// A recursive function to find the maximum rectangular area.
// It uses segment tree 'st' to find the minimum value in hist[l..r]
int getMaxAreaRec(int *hist, int *st, int n, int l, int r)
{
// Base cases
if (l > r) return INT_MIN;
if (l == r) return hist[l];
// Find index of the minimum value in given range
// This takes O(Logn)time
int m = RMQ(hist, st, n, l, r);
/* Return maximum of following three possible cases
a) Maximum area in Left of min value (not including the min)
a) Maximum area in right of min value (not including the min)
c) Maximum area including min */
return max(getMaxAreaRec(hist, st, n, l, m-1),
getMaxAreaRec(hist, st, n, m+1, r),
(r-l+1)*(hist[m]) );
}
// The main function to find max area
int getMaxArea(int hist[], int n)
{
// Build segment tree from given array. This takes
// O(n) time
int *st = constructST(hist, n);
// Use recursive utility function to find the
// maximum area
return getMaxAreaRec(hist, st, n, 0, n-1);
}
// Driver program to test above functions
int main()
{
int hist[] = {6, 1, 5, 4, 5, 2, 6};
int n = sizeof(hist)/sizeof(hist[0]);
cout << "Maximum area is " << getMaxArea(hist, n);
return 0;
}
Java
// A Divide and Conquer Program to find maximum rectangular area in a histogram
import java.util.*;
class GFG{
static int[] hist;
static int[] st;
// A utility function to find minimum of three integers
static int max(int x, int y, int z)
{ return Math.max(Math.max(x, y), z); }
// A utility function to get minimum of two numbers in hist[]
static int minVal(int i, int j)
{
if (i == -1) return j;
if (j == -1) return i;
return (hist[i] < hist[j])? i : j;
}
// A utility function to get the middle index from corner indexes.
static int getMid(int s, int e)
{ return s + (e -s)/2; }
/* A recursive function to get the index of minimum value in a given range of
indexes. The following are parameters for this function.
hist -. Input array for which segment tree is built
st -. Pointer to segment tree
index -. Index of current node in the segment tree. Initially 0 is
passed as root is always at index 0
ss & se -. Starting and ending indexes of the segment represented by
current node, i.e., st[index]
qs & qe -. Starting and ending indexes of query range */
static int RMQUtil( int ss, int se, int qs, int qe, int index)
{
// If segment of this node is a part of given range, then return the
// min of the segment
if (qs <= ss && qe >= se)
return st[index];
// If segment of this node is outside the given range
if (se < qs || ss > qe)
return -1;
// If a part of this segment overlaps with the given range
int mid = getMid(ss, se);
return minVal( RMQUtil(ss, mid, qs, qe, 2*index+1),
RMQUtil( mid+1, se, qs, qe, 2*index+2));
}
// Return index of minimum element in range from index qs (query start) to
// qe (query end). It mainly uses RMQUtil()
static int RMQ( int n, int qs, int qe)
{
// Check for erroneous input values
if (qs < 0 || qe > n-1 || qs > qe)
{
System.out.print("Invalid Input");
return -1;
}
return RMQUtil( 0, n-1, qs, qe, 0);
}
// A recursive function that constructs Segment Tree for hist[ss..se].
// si is index of current node in segment tree st
static int constructSTUtil(int ss, int se, int si)
{
// If there is one element in array, store it in current node of
// segment tree and return
if (ss == se)
return (st[si] = ss);
// If there are more than one elements, then recur for left and
// right subtrees and store the minimum of two values in this node
int mid = getMid(ss, se);
st[si] = minVal( constructSTUtil( ss, mid, si*2+1),
constructSTUtil( mid+1, se, si*2+2));
return st[si];
}
/* Function to construct segment tree from given array. This function
allocates memory for segment tree and calls constructSTUtil() to
fill the allocated memory */
static void constructST(int n)
{
// Allocate memory for segment tree
int x = (int)(Math.ceil(Math.log(n))); //Height of segment tree
int max_size = 2*(int)Math.pow(2, x) - 1; //Maximum size of segment tree
st = new int[max_size*2];
// Fill the allocated memory st
constructSTUtil( 0, n-1, 0);
// Return the constructed segment tree
// return st;
}
// A recursive function to find the maximum rectangular area.
// It uses segment tree 'st' to find the minimum value in hist[l..r]
static int getMaxAreaRec( int n, int l, int r)
{
// Base cases
if (l > r) return Integer.MIN_VALUE;
if (l == r) return hist[l];
// Find index of the minimum value in given range
// This takes O(Logn)time
int m = RMQ( n, l, r);
/* Return maximum of following three possible cases
a) Maximum area in Left of min value (not including the min)
a) Maximum area in right of min value (not including the min)
c) Maximum area including min */
return max(getMaxAreaRec( n, l, m - 1),
getMaxAreaRec( n, m + 1, r),
(r - l + 1)*(hist[m]) );
}
// The main function to find max area
static int getMaxArea( int n)
{
// Build segment tree from given array. This takes
// O(n) time
constructST(n);
// Use recursive utility function to find the
// maximum area
return getMaxAreaRec( n, 0, n - 1);
}
// Driver program to test above functions
public static void main(String[] args)
{
int[] a = {6, 1, 5, 4, 5, 2, 6};
int n = a.length;
hist = new int[n];
hist = a;
System.out.print("Maximum area is " + getMaxArea(n));
}
}
// This code is contributed by Rajput-Ji
Python
# Python3 program for range minimum
# query using segment tree
# modified to return index of minimum instead of minimum itself
# for further reference link
# https://www.geeksforgeeks.org/segment-tree-set-1-range-minimum-query/
#-------------------------------------------------------------------------
from math import ceil,log2;
# A utility function to get
# minimum of two numbers
def minVal(hist,x, y) :
if x==-1:
return y
if y==-1:
return x
return x if (hist[x] < hist[y]) else y;
# A utility function to get the
# middle index from corner indexes.
def getMid(s, e) :
return s + (e - s) // 2;
""" A recursive function to get the
minimum value in a given range
of array indexes. The following
are parameters for this function.
st --> Pointer to segment tree
index --> Index of current node in the
segment tree. Initially 0 is
passed as root is always at index 0
ss & se --> Starting and ending indexes
of the segment represented
by current node, i.e., st[index]
qs & qe --> Starting and ending indexes of query range """
def RMQUtil( hist,st, ss, se, qs, qe, index) :
# If segment of this node is a part
# of given range, then return
# the min of the segment
if (qs <= ss and qe >= se) :
return st[index];
# If segment of this node
# is outside the given range
if (se < qs or ss > qe) :
return -1;
# If a part of this segment
# overlaps with the given range
mid = getMid(ss, se);
return minVal(hist,RMQUtil(hist,st, ss, mid, qs,
qe, 2 * index + 1),
RMQUtil(hist,st, mid + 1, se,
qs, qe, 2 * index + 2));
# Return minimum of elements in range
# from index qs (query start) to
# qe (query end). It mainly uses RMQUtil()
def RMQ( hist,st, n, qs, qe) :
# Check for erroneous input values
if (qs < 0 or qe > n - 1 or qs > qe) :
print("Invalid Input");
return -1;
return RMQUtil(hist,st, 0, n - 1, qs, qe, 0);
# A recursive function that constructs
# Segment Tree for array[ss..se].
# si is index of current node in segment tree st
def constructSTUtil(hist, ss, se, st, si) :
# If there is one element in array,
# store it in current node of
# segment tree and return
if (ss == se) :
st[si] = ss;
return st[si];
# If there are more than one elements,
# then recur for left and right subtrees
# and store the minimum of two values in this node
mid = getMid(ss, se);
st[si] = minVal(hist,constructSTUtil(hist, ss, mid,
st, si * 2 + 1),
constructSTUtil(hist, mid + 1, se,
st, si * 2 + 2));
return st[si];
"""Function to construct segment tree
from given array. This function allocates
memory for segment tree and calls constructSTUtil()
to fill the allocated memory """
def constructST( hist, n) :
# Allocate memory for segment tree
# Height of segment tree
x = (int)(ceil(log2(n)));
# Maximum size of segment tree
max_size = 2 * (int)(2**x) - 1;
st = [0] * (max_size);
# Fill the allocated memory st
constructSTUtil(hist, 0, n - 1, st, 0);
# Return the constructed segment tree
return st;
#----------------------------------------------------------------
# main program
# Python3 program using Divide and Conquer
# to find maximum rectangular area under a histogram
def max_area_histogram(hist):
area=0
#initialize area
st = constructST(hist, len(hist))
# construct the segment tree
try:
# try except block is generally used in this way
# to suppress all type of exceptions raised.
def fun(left,right):
# this function "fun" calculates area
# recursively between indices left and right
nonlocal area
# global area won't work here as
# variable area is defined inside function
# not in main().
if left==right:
return
# the recursion has reached end
index = RMQ(hist,st, len(hist), left, right-1)
# RMQ function returns index
# of minimum value
# in the range of [left,right-1]
# can also be found by using min() but
# results in O(n) instead of O(log n) for traversing
area=max(area,hist[index]*(right-left))
# calculate area with minimum above
fun(index+1,right)
fun(left,index)
# initiate further recursion
return
fun(0,len(hist))
# initializes the recursion
return(area)
# return the max area to calling function
# in this case "print"
except:
pass
# Driver Code
hist = [6, 2, 5, 4, 5, 1, 6]
print("Maximum area is",
max_area_histogram(hist))
# This code is contributed
# by Vishnudev C.
C#
// C# code to implement the approach
using System;
using System.Numerics;
using System.Collections.Generic;
public class GFG {
static int[] hist;
static int[] st;
// A utility function to find minimum of three integers
static int max(int x, int y, int z)
{ return Math.Max(Math.Max(x, y), z); }
// A utility function to get minimum of two numbers in hist[]
static int minVal(int i, int j)
{
if (i == -1) return j;
if (j == -1) return i;
return (hist[i] < hist[j])? i : j;
}
// A utility function to get the middle index from corner indexes.
static int getMid(int s, int e)
{ return s + (e -s)/2; }
/* A recursive function to get the index of minimum value in a given range of
indexes. The following are parameters for this function.
hist -. Input array for which segment tree is built
st -. Pointer to segment tree
index -. Index of current node in the segment tree. Initially 0 is
passed as root is always at index 0
ss & se -. Starting and ending indexes of the segment represented by
current node, i.e., st[index]
qs & qe -. Starting and ending indexes of query range */
static int RMQUtil( int ss, int se, int qs, int qe, int index)
{
// If segment of this node is a part of given range, then return the
// min of the segment
if (qs <= ss && qe >= se)
return st[index];
// If segment of this node is outside the given range
if (se < qs || ss > qe)
return -1;
// If a part of this segment overlaps with the given range
int mid = getMid(ss, se);
return minVal( RMQUtil(ss, mid, qs, qe, 2*index+1),
RMQUtil( mid+1, se, qs, qe, 2*index+2));
}
// Return index of minimum element in range from index qs (query start) to
// qe (query end). It mainly uses RMQUtil()
static int RMQ( int n, int qs, int qe)
{
// Check for erroneous input values
if (qs < 0 || qe > n-1 || qs > qe)
{
Console.Write("Invalid Input");
return -1;
}
return RMQUtil( 0, n-1, qs, qe, 0);
}
// A recursive function that constructs Segment Tree for hist[ss..se].
// si is index of current node in segment tree st
static int constructSTUtil(int ss, int se, int si)
{
// If there is one element in array, store it in current node of
// segment tree and return
if (ss == se)
return (st[si] = ss);
// If there are more than one elements, then recur for left and
// right subtrees and store the minimum of two values in this node
int mid = getMid(ss, se);
st[si] = minVal( constructSTUtil( ss, mid, si*2+1),
constructSTUtil( mid+1, se, si*2+2));
return st[si];
}
/* Function to construct segment tree from given array. This function
allocates memory for segment tree and calls constructSTUtil() to
fill the allocated memory */
static void constructST(int n)
{
// Allocate memory for segment tree
int x = (int)(Math.Ceiling(Math.Log(n))); //Height of segment tree
int max_size = 2*(int)Math.Pow(2, x) - 1; //Maximum size of segment tree
st = new int[max_size*2];
// Fill the allocated memory st
constructSTUtil( 0, n-1, 0);
// Return the constructed segment tree
// return st;
}
// A recursive function to find the maximum rectangular area.
// It uses segment tree 'st' to find the minimum value in hist[l..r]
static int getMaxAreaRec( int n, int l, int r)
{
// Base cases
if (l > r) return Int32.MinValue;
if (l == r) return hist[l];
// Find index of the minimum value in given range
// This takes O(Logn)time
int m = RMQ( n, l, r);
/* Return maximum of following three possible cases
a) Maximum area in Left of min value (not including the min)
a) Maximum area in right of min value (not including the min)
c) Maximum area including min */
return max(getMaxAreaRec( n, l, m - 1),
getMaxAreaRec( n, m + 1, r),
(r - l + 1)*(hist[m]) );
}
// The main function to find max area
static int getMaxArea( int n)
{
// Build segment tree from given array. This takes
// O(n) time
constructST(n);
// Use recursive utility function to find the
// maximum area
return getMaxAreaRec( n, 0, n - 1);
}
// Driver Code
public static void Main(string[] args)
{
int[] a = {6, 1, 5, 4, 5, 2, 6};
int n = a.Length;
hist = new int[n];
hist = a;
Console.WriteLine("Maximum area is " + getMaxArea(n));
}
}
Output
Maximum area is 12
Time Complexity: O(N log N)
Auxiliary Space: O(N)
