This method mostly serves as an optimization over the last one. The optimizations follow from below observations.
We pop one item from the stack and mark current item as next smaller of it while computing next smaller element. Here, one significant note is the item below each item in the stack—the former smaller element. We thus do not have to specifically compute previous smaller.
The thorough implementation steps are listed here.
- Generate an empty stack.
- Starting from the first bar, proceed for each bar hist[i] where “i” ranges from 0 to n-1.
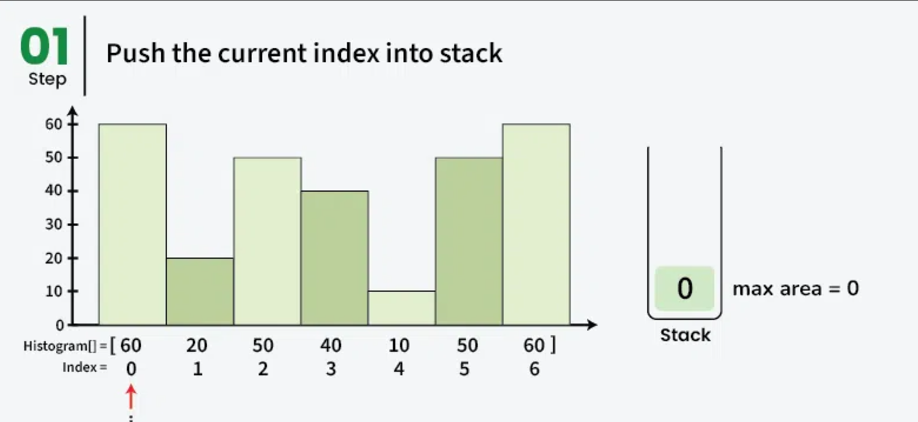
- Push “i” to stack if the stack is empty or hist[i] is greater than the bar at top of the stack.
- Should this bar be less than the top of the stack, keep eliminating the top while the top of the stack remains higher.
- Allow the deleted bar to be hist[tp]. With hist[tp] as the smallest bar, get the rectangle’s area.
- The “left index” for hist[tp] is the item past (prior to tp) from the stack; the “right index” is “i,” the current index.
- Should the stack not be empty, remove one bar at a time using step (2.2 and 2.3) for each eliminated bar.
- The above technique is illustrated below:
C++
#include <bits/stdc++.h>
using namespace std;
int getMaxArea(vector<int>& arr) {
int n = arr.size();
stack<int> s;
int res = 0;
int tp, curr;
for (int i = 0; i < n; i++) {
while (!s.empty() && arr[s.top()] >= arr[i]) {
// The popped item is to be considered as the
// smallest element of the histogram
tp = s.top();
s.pop();
// For the popped item previous smaller element is
// just below it in the stack (or current stack top)
// and next smaller element is i
int width = s.empty() ? i : i - s.top() - 1;
res = max(res, arr[tp] * width);
}
s.push(i);
}
// For the remaining items in the stack, next smaller does
// not exist. Previous smaller is the item just below in
// stack.
while (!s.empty()) {
tp = s.top(); s.pop();
curr = arr[tp] * (s.empty() ? n : n - s.top() - 1);
res = max(res, curr);
}
return res;
}
int main() {
vector<int> arr = {60, 20, 50, 40, 10, 50, 60};
cout << getMaxArea(arr);
return 0;
}C
#include <stdio.h>
#include <stdlib.h>
// Stack structure
struct Stack {
int top;
int capacity;
int* array;
};
// Function to create a stack
struct Stack* createStack(int capacity) {
struct Stack* stack = (struct Stack*)
malloc(sizeof(struct Stack));
stack->capacity = capacity;
stack->top = -1;
stack->array = (int*)malloc(stack->capacity * sizeof(int));
return stack;
}
int isEmpty(struct Stack* stack) {
return stack->top == -1;
}
void push(struct Stack* stack, int item) {
stack->array[++stack->top] = item;
}
int pop(struct Stack* stack) {
return stack->array[stack->top--];
}
int peek(struct Stack* stack) {
return stack->array[stack->top];
}
// Function to calculate the maximum rectangular area
int getMaxArea(int arr[], int n) {
struct Stack* s = createStack(n);
int res = 0, tp, curr;
// Traverse all bars of the histogram
for (int i = 0; i < n; i++) {
// Process the stack while the current element
// is smaller than the element corresponding to
// the top of the stack
while (!isEmpty(s) && arr[peek(s)] >= arr[i]) {
tp = pop(s);
// Calculate width and update result
int width = isEmpty(s) ? i : i - peek(s) - 1;
res = (res > arr[tp] * width) ? res : arr[tp] * width;
}
push(s, i);
}
// Process remaining elements in the stack
while (!isEmpty(s)) {
tp = pop(s);
curr = arr[tp] * (isEmpty(s) ? n : n - peek(s) - 1);
res = (res > curr) ? res : curr;
}
return res;
}
int main() {
int arr[] = {60, 20, 50, 40, 10, 50, 60};
int n = sizeof(arr) / sizeof(arr[0]);
printf("%d\n", getMaxArea(arr, n));
return 0;
}Java
import java.util.Stack;
class GfG {
public static int getMaxArea(int[] arr) {
int n = arr.length;
Stack<Integer> s = new Stack<>();
int res = 0, tp, curr;
for (int i = 0; i < n; i++) {
// Process the stack while the current element
// is smaller than the element corresponding to
// the top of the stack
while (!s.isEmpty() && arr[s.peek()] >= arr[i]) {
// The popped item is to be considered as the
// smallest element of the histogram
tp = s.pop();
// For the popped item, previous smaller element
// is just below it in the stack (or current stack
// top) and next smaller element is i
int width = s.isEmpty() ? i : i - s.peek() - 1;
// Update the result if needed
res = Math.max(res, arr[tp] * width);
}
s.push(i);
}
// For the remaining items in the stack, next smaller does
// not exist. Previous smaller is the item just below in
// the stack.
while (!s.isEmpty()) {
tp = s.pop();
curr = arr[tp] * (s.isEmpty() ? n : n - s.peek() - 1);
res = Math.max(res, curr);
}
return res;
}
public static void main(String[] args) {
int[] arr = {60, 20, 50, 40, 10, 50, 60};
System.out.println(getMaxArea(arr));
}
}Python
def get_max_area(arr):
n = len(arr)
s = []
res = 0
for i in range(n):
# Process the stack while the current element
# is smaller than the element corresponding to
# the top of the stack
while s and arr[s[-1]] >= arr[i]:
# The popped item is to be considered as the
# smallest element of the histogram
tp = s.pop()
# For the popped item, the previous smaller
# element is just below it in the stack (or
# the current stack top) and the next smaller
# element is i
width = i if not s else i - s[-1] - 1
# Update the result if needed
res = max(res, arr[tp] * width)
s.append(i)
# For the remaining items in the stack, next smaller does
# not exist. Previous smaller is the item just below in
# the stack.
while s:
tp = s.pop()
width = n if not s else n - s[-1] - 1
res = max(res, arr[tp] * width)
return res
if __name__ == "__main__":
arr = [60, 20, 50, 40, 10, 50, 60]
print(get_max_area(arr))Output
100
