Merge Overlapping Intervals-Checking Last Merged Interval

Under the former method, we iteratively search throughout all the remaining ranges until the end for every range we are looking for potential overlaps. Examining just those intervals that coincide with the latest merged interval will help us maximize this. The intervals will be arranged according on starting point, hence if we come across an interval whose starting time falls outside the last merged interval, all subsequent intervals will likewise lie outside it.

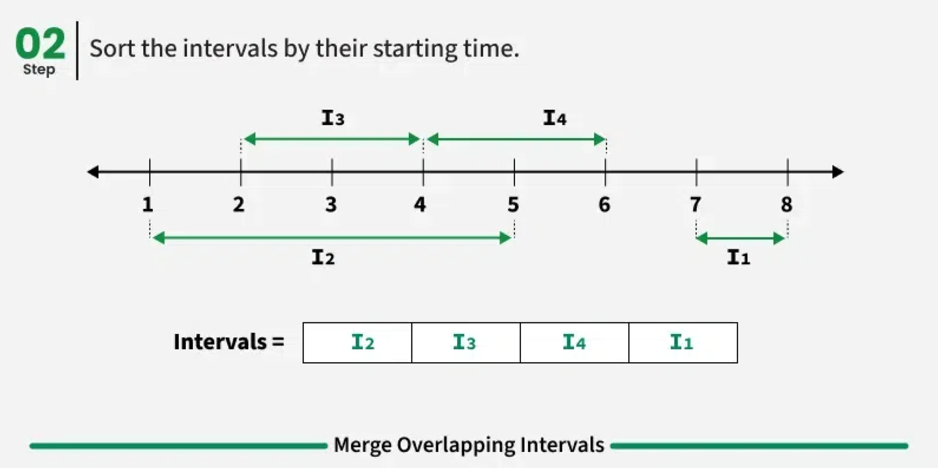
First, one sorts the intervals according to their initial places intuitively. Comparing each interval with the last merged interval lets us quickly spot overlapping intervals. Iterate over every interval now; if the current interval crosses the last merged interval, combine both of them. Otherwise, add the resultant combined interval.

C++

// C++ Code to Merge Overlapping Intervals by checking 
// overlapping intervals only

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

vector<vector<int>> mergeOverlap(vector<vector<int>>& arr) {

    // Sort intervals based on start values
    sort(arr.begin(), arr.end());
  
    vector<vector<int>> res;
    res.push_back(arr[0]);

    for (int i = 1; i < arr.size(); i++) {
        vector<int>& last = res.back();
        vector<int>& curr = arr[i];

        // If current interval overlaps with the last merged
        // interval, merge them 
        if (curr[0] <= last[1]) 
            last[1] = max(last[1], curr[1]);
        else 
            res.push_back(curr);
    }

    return res;
}

int main() {
    vector<vector<int>> arr = {{7, 8}, {1, 5}, {2, 4}, {4, 6}};
    vector<vector<int>> res = mergeOverlap(arr);

      for (vector<int>& interval: res) 
        cout << interval[0] << " " << interval[1] << endl;
 
    return 0;
}

Java

// Java Code to Merge Overlapping Intervals by checking 
// overlapping intervals only

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

class GfG {

    static List<int[]> mergeOverlap(int[][] arr) {
        
        // Sort intervals based on start values
        Arrays.sort(arr, (a, b) -> Integer.compare(a[0], b[0]));

        List<int[]> res = new ArrayList<>();
        res.add(new int[]{arr[0][0], arr[0][1]});

        for (int i = 1; i < arr.length; i++) {
            int[] last = res.get(res.size() - 1);
            int[] curr = arr[i];

            // If current interval overlaps with the last merged 
            // interval, merge them 
            if (curr[0] <= last[1]) 
                last[1] = Math.max(last[1], curr[1]);
            else 
                res.add(new int[]{curr[0], curr[1]});
        }

        return res;
    }

    public static void main(String[] args) {
        int[][] arr = {{7, 8}, {1, 5}, {2, 4}, {4, 6}};
        List<int[]> res = mergeOverlap(arr);

        for (int[] interval : res) 
            System.out.println(interval[0] + " " + interval[1]);
    }
}

Python

# Python Code to Merge Overlapping Intervals by checking 
# overlapping intervals only

def mergeOverlap(arr):
    
    # Sort intervals based on start values
    arr.sort()

    res = []
    res.append(arr[0])

    for i in range(1, len(arr)):
        last = res[-1]
        curr = arr[i]

        # If current interval overlaps with the last merged
        # interval, merge them 
        if curr[0] <= last[1]:
            last[1] = max(last[1], curr[1])
        else:
            res.append(curr)

    return res

if __name__ == "__main__":
    arr = [[7, 8], [1, 5], [2, 4], [4, 6]]
    res = mergeOverlap(arr)

    for interval in res:
        print(interval[0], interval[1])

C#

// C# Code to Merge Overlapping Intervals by checking 
// overlapping intervals only

using System;
using System.Collections.Generic;

class GfG {
    static List<int[]> mergeOverlap(int[][] arr) {
        
        // Sort intervals based on start values
        Array.Sort(arr, (a, b) => a[0].CompareTo(b[0]));

        List<int[]> res = new List<int[]>();
        res.Add(new int[] { arr[0][0], arr[0][1] });

        for (int i = 1; i < arr.Length; i++) {
            int[] last = res[res.Count - 1];
            int[] curr = arr[i];

            // If current interval overlaps with the last merged
            // interval, merge them 
            if (curr[0] <= last[1])
                last[1] = Math.Max(last[1], curr[1]);
            else
                res.Add(new int[] { curr[0], curr[1] });
        }

        return res;
    }

    static void Main() {
        int[][] arr = new int[][] {
            new int[] { 7, 8 },
            new int[] { 1, 5 },
            new int[] { 2, 4 },
            new int[] { 4, 6 }
        };

        List<int[]> res = mergeOverlap(arr);

        foreach (int[] interval in res)
            Console.WriteLine(interval[0] + " " + interval[1]);
    }
}

Output

1 6
7 8