We have covered Kruskal’s method for minimum spanning trees in introduction. Prim’s method is a Greedy algorithm, same with Kruskal’s one. Starting with a single node, this algorithm explores all the related edges along the path by moving through multiple nearby nodes always.
Starting with an empty spanning tree, the method proceeds Two sets of vertices are meant to be maintained. The MST already includes the vertices in the first set; the other set comprises the vertices not yet included. It chooses the minimum weight edge from all the edges that link the two sets at each turn. Following edge selection, it moves the other edge endpoint to the set including MST.
In graph theory, cut in graph theory is the collection of edges linking two sets of vertices in a graph. Thus, identify a cut at each stage of Prim’s algorithm, choose the minimal weight edge from the cut, and add this vertex to MST Set (the set comprising already mentioned vertices).
Prim’s Algorithm’s mechanism is what?
One may characterize the operation of Prim’s method by means of the following steps:
- First step: Choose an arbitrary vertex to start the MST.
- Following steps 3 through 5 will help you find vertices not included in the MST—also referred to as fringe vertex.
- Look for edges linking any tree vertex to the fringe vertices in third step.
- Fourth step: among these edges, determine the minimum.
- Should the selected edge not create any cycle, add it to the MST.
- Step 6: Come back to exit and MST
Note: We can split the vertices into two sets [one set comprises the vertices included in MST and the other comprises the peripheral vertices.] to identify a cycle.
Primary’s Algorithm Illustration
Let us use the following graph as an illustration for which we must determine the Minimum Spanning Tree (MST).

First we choose an arbitrary vertex to serve as the Minimum Spanning Tree’s starting vertex. Our starting vertex here is vertex 0.
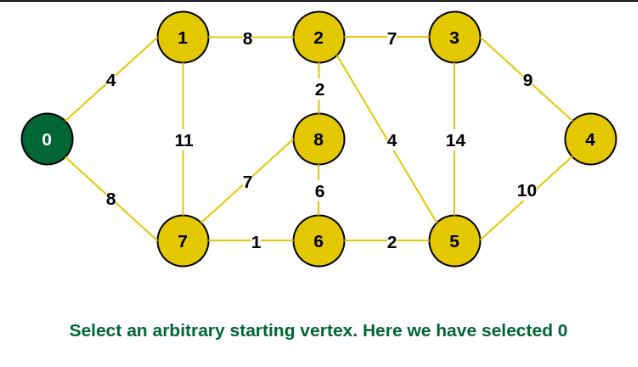
The edges {0, 1} and {0, 7} define all the edges linking the incomplete MST and other vertices in second step. Between these two the edge with least weight is {0, 1}. Thus, include in the MST the edge and vertex 1.

The edges joining the incomplete MST to other vertices are {0, 7}, {1, 7} and {1, 2}. Of these edges, only 8 has minimum weight; these are edges {0, 7} and {1, 2}. Let us thus consider the MST’s vertex 7 and the edge {0, 7}. [We also might have included vertex 2 in the MST and edge {1, 2}.
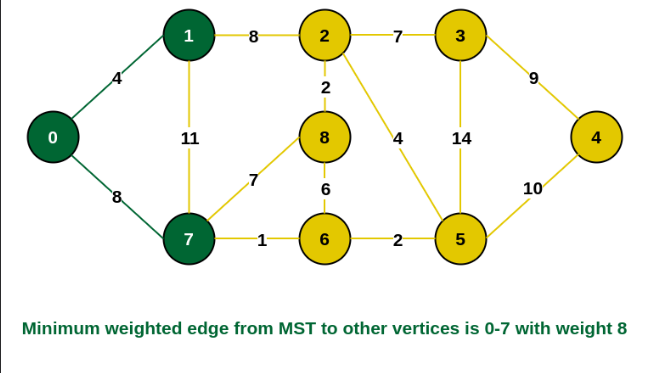
The edges {1, 2}, {7, 6} and {7, 8} link the incomplete MST with the fringe vertices. As the MST has the least weight—that is, one—add the vertex 6 and the edge {7, 6}.
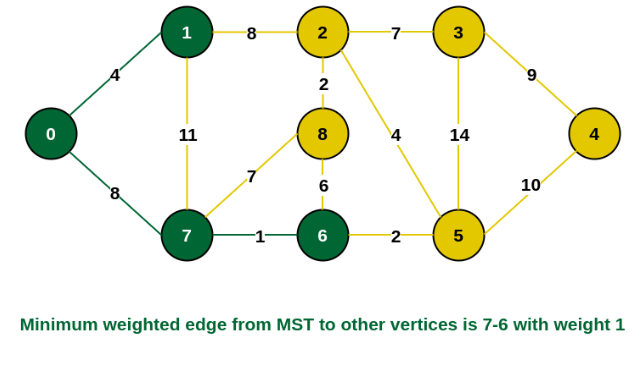
Step 5:
The connecting edges now are {7, 8}, {1, 2}, {6, 8} and {6, 5}. Include edge {6, 5} and vertex 5 in the MST as the edge has the minimum weight (i.e., 2) among them.

Step 6: With the minimum weight among the present connecting edges is {5, 2}. Thus, incorporate that edge and vertex two in the MST.

The connecting edges between the other edges and the unfinished MST are {2, 8}, {2, 3}, {5, 3} and {5, 4}. Edge {2, 8} with weight 2. has least weight edge. Thus, incorporate in the MST this edge and the vertex number eight.

Step 8: See here that both the minimum weight of the edges {7, 8} and {2, 3} is similar. Nevertheless, 7 is already included into MST. We shall so take into account the edge {2, 3} and incorporate vertex 3 in the MST.

Step 9: There is just one vertex 4 left to be added. From the incomplete MST to 4 the minimum weighted edge is {3, 4}.
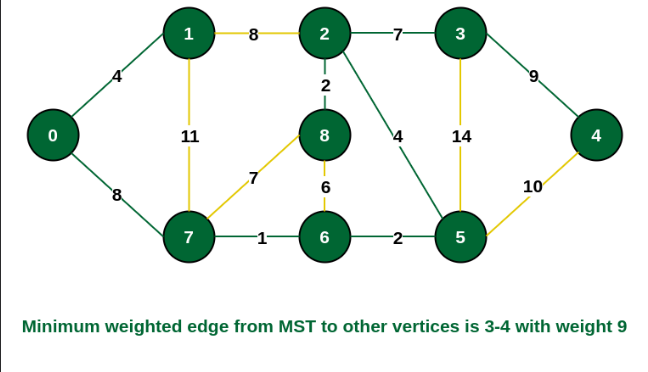
The MST has a final structure like this with weights (4 + 8 + 1 + 2 + 4 + 2 + 7 + 9) = 37 on its edges.

Prim’s Algorithm implementation:
Use the above described Prim’s Algorithm to determine MST of a graph following the provided guidelines:
- Make a set mstSet to monitor already included vertices in MST.
- Give every input graph’s vertex a key value. Set all main values as INFINITE initially. Give the first vertex zero for the key value so it will be chosen first.
- mstSet excludes all vertices, though.
- Choose a vertex u with a minimum key value not found in mstSet.
- List u among the mstSet.
- Update the key value of every adjacent vertex of u. Go through all of the nearby vertices to change the main values.
- Update the key value as the weight of edge u-v if its weight is smaller than the previous key value of v.
- Choosing the minimum weight edge from the cut is the aim of employing key values. The main values are applied exclusively for vertices not yet included in MST; their key value denotes the minimal weight edges tying them to the collection of vertices included in MST.
Analysis of Complexity of Prim’s Algorithm:
Time Complexity: O(V2) By means of a binary heap, Prim’s algorithm’s time complexity can be lowered to O(E * logV) should the input graph be presented using an adjacency list. In this implementation, we always start from the graph’s root considering the spanning tree.
Auxiliary Space: V(O)
Adjacent List Representation (of Graph) with Priority Queue Intuition Optimized Implementation
- We convert the adjacency matrix into adjacency list with ArrayList>. List of lists in Java, Python, and Java in Java, C++, array of vectors,
- Then design a Pair class to keep the vertex and weight.
- We arrange the list lowest weight first.
- We establish a priority queue and forward the first vertices together with their weight.
- Then just follow its edges and save the least weight in a variable known as ans.
- At last, at last following all the vertices, we return the answer.
Prim’s method for minimal spanning tree (MST) computation:
- The MST in a linked, weighted graph is assured to be found by Prim’s algorithm.
- With a binary heap or Fibonacci heap—where E is the number of edges and V is the number of vertices—its temporal complexity is O(E log V.
- Comparatively to some other MST techniques, this is a quite straightforward algorithm to grasp and apply.
Negative aspects:
- Prim’s method, which involves iterating over all edges at least once, can be slow on thick graphs with numerous edges, much as Kruskal’s method can be.
- Prim’s method depends on a priority queue, which for very big graphs slows down the algorithm and consumes additional memory.
- Starting node selection might influence MST output, which might not be desired in some uses.
