[Space Optimized Approach]: Using Boundary Traversal – O(m*n) Time and O(1) Space
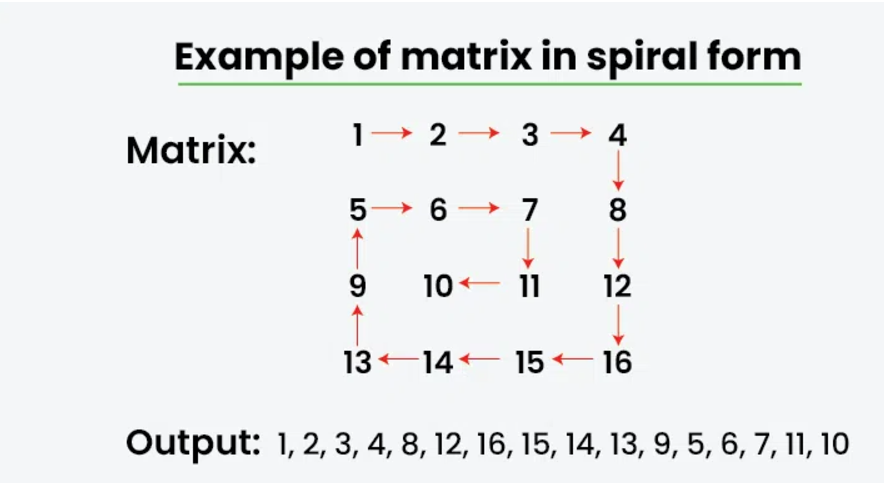
Divining the matrix into loops or boundaries allows us to print it in a spiral sequence. First we print the outside boundary elements then we move inward to print the elements of the inner bounds.
- Specify the matrix’s top, bottom, left, and right borders via variables.
- Print the top row from left to right then raise top.
- Print the right column from top to bottom then reduce right.
- Check whether limits have been crossed; if not, print the bottom row from right to left and drop bottom.
- Print the left column from bottom to top incrementing left.
- Keep on until all limits are broken.
C++
#include <bits/stdc++.h>
using namespace std;
// Function to perform spiral order printing of a matrix
void spiralPrint(int m, int n, vector<vector<int> >&mat) {
// Initialize boundaries
int top = 0, bottom = m - 1, left = 0, right = n - 1;
// Iterate until all elements are printed
while (top <= bottom && left <= right) {
// Print top row from left to right
for (int i = left; i <= right; ++i) {
cout << mat[top][i] << " ";
}
top++;
// Print right column from top to bottom
for (int i = top; i <= bottom; ++i) {
cout << mat[i][right] << " ";
}
right--;
// Print bottom row from right to left (if exists)
if (top <= bottom) {
for (int i = right; i >= left; --i) {
cout << mat[bottom][i] << " ";
}
bottom--;
}
// Print left column from bottom to top (if exists)
if (left <= right) {
for (int i = bottom; i >= top; --i) {
cout << mat[i][left] << " ";
}
left++;
}
}
}
int main() {
vector<vector<int> > mat = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 } };
spiralPrint(mat.size(), mat[0].size(), mat);
return 0;
}Java
import java.util.*;
class GfG {
// Function to perform spiral order printing of a matrix
static void spiralPrint(int m, int n, int[][] mat) {
// Initialize boundaries
int top = 0, bottom = m - 1, left = 0,
right = n - 1;
// Iterate until all elements are printed
while (top <= bottom && left <= right) {
// Print top row from left to right
for (int i = left; i <= right; ++i) {
System.out.print(mat[top][i] + " ");
}
top++;
// Print right column from top to bottom
for (int i = top; i <= bottom; ++i) {
System.out.print(mat[i][right] + " ");
}
right--;
// Print bottom row from right to left (if
// exists)
if (top <= bottom) {
for (int i = right; i >= left; --i) {
System.out.print(mat[bottom][i] + " ");
}
bottom--;
}
// Print left column from bottom to top (if
// exists)
if (left <= right) {
for (int i = bottom; i >= top; --i) {
System.out.print(mat[i][left] + " ");
}
left++;
}
}
}
public static void main(String[] args) {
int[][] mat = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 } };
spiralPrint(mat.length, mat[0].length,
mat);
}
}Python
def spiralPrint(m, n, mat):
# Initialize boundaries
top, bottom, left, right = 0, m - 1, 0, n - 1
# Iterate until all elements are printed
while top <= bottom and left <= right:
# Print top row from left to right
for i in range(left, right + 1):
print(mat[top][i], end=" ")
top += 1
# Print right column from top to bottom
for i in range(top, bottom + 1):
print(mat[i][right], end=" ")
right -= 1
# Print bottom row from right to left (if exists)
if top <= bottom:
for i in range(right, left - 1, -1):
print(mat[bottom][i], end=" ")
bottom -= 1
# Print left column from bottom to top (if exists)
if left <= right:
for i in range(bottom, top - 1, -1):
print(mat[i][left], end=" ")
left += 1
if __name__ == "__main__":
mat = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]
]
spiralPrint(len(mat), len(mat[0]), mat)c#
using System;
class GfG {
// Function to perform spiral order printing of a matrix
static void SpiralPrint(int m, int n, int[,] mat) {
// Initialize boundaries
int top = 0, bottom = m - 1, left = 0, right = n - 1;
// Iterate until all elements are printed
while (top <= bottom && left <= right) {
// Print top row from left to right
for (int i = left; i <= right; ++i) {
Console.Write(mat[top, i] + " ");
}
top++;
// Print right column from top to bottom
for (int i = top; i <= bottom; ++i) {
Console.Write(mat[i, right] + " ");
}
right--;
// Print bottom row from right to left (if exists)
if (top <= bottom) {
for (int i = right; i >= left; --i) {
Console.Write(mat[bottom, i] + " ");
}
bottom--;
}
// Print left column from bottom to top (if exists)
if (left <= right) {
for (int i = bottom; i >= top; --i) {
Console.Write(mat[i, left] + " ");
}
left++;
}
}
}
static void Main() {
int[,] mat = {
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 }
};
SpiralPrint(mat.GetLength(0), mat.GetLength(1), mat);
}
}JavaScript
// Function to perform spiral order printing of a matrix
function spiralPrint(m, n, a) {
// Initialize boundaries
let top = 0, bottom = m - 1, left = 0, right = n - 1;
// Iterate until all elements are printed
while (top <= bottom && left <= right) {
// Print top row from left to right
for (let i = left; i <= right; ++i) {
console.log(mat[top][i] + " ");
}
top++;
// Print right column from top to bottom
for (let i = top; i <= bottom; ++i) {
console.log(mat[i][right] + " ");
}
right--;
// Print bottom row from right to left (if exists)
if (top <= bottom) {
for (let i = right; i >= left; --i) {
console.log(mat[bottom][i] + " ");
}
bottom--;
}
// Print left column from bottom to top (if exists)
if (left <= right) {
for (let i = bottom; i >= top; --i) {
console.log(mat[i][left] + " ");
}
left++;
}
}
}
let mat = [
[ 1, 2, 3, 4 ], [ 5, 6, 7, 8 ], [ 9, 10, 11, 12 ],
[ 13, 14, 15, 16 ]
];
spiralPrint(mat.length, mat[0].length, mat);Output
1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10
Time Complexity: O(m*n), where m and n are the number of rows and columns of the given matrix respectively.
Auxiliary Space: O(1).
