Trapping Rain Water Problem-Computing prefix and suffix max

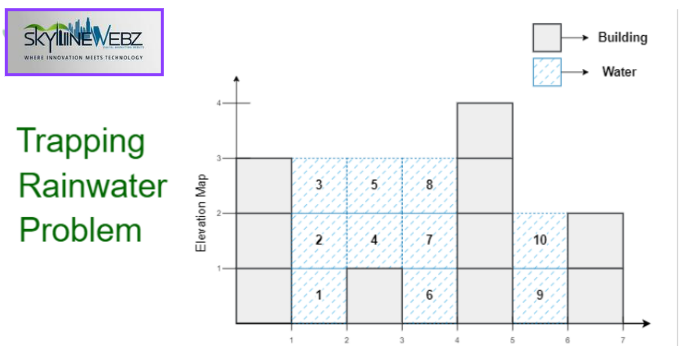
Under the former method, for every element we required to determine the highest element on the left and the right.

Consequently, to lower the temporal complexity:

First we compute and save the highest bar on the left and right for every element—say placed in arrays left[] and right[].
Then iterate the array using the computed values to determine the water stored in this index—that is, the same as ( min(left[i], right[i]) – arr[i]).

C++

// C++ program to find maximum amount of water
// that can be trapped within given set of bars.
#include <bits/stdc++.h>
using namespace std;

int findWater(vector<int>& arr)
{
    int n = arr.size();

    // Left[i] contains height of tallest bar to the
    // left of i'th bar including itself
    vector<int> left(n);

    // Right[i] contains height of tallest bar to
    // the right of i'th bar including itself
    vector<int> right(n);

    // Initialize result
    int res = 0;

    // Fill left array
    left[0] = arr[0];
    for (int i = 1; i < n; i++)
        left[i] = max(left[i - 1], arr[i]);

    // Fill right array
    right[n - 1] = arr[n - 1];
    for (int i = n - 2; i >= 0; i--)
        right[i] = max(right[i + 1], arr[i]);

    // Calculate the accumulated water element by element
    for (int i = 1; i < n - 1; i++) {
        int minOf2 = min(left[i - 1], right[i + 1]);
        if (minOf2 > arr[i]) {
            res += minOf2 - arr[i];
        }
    }

    return res;
}

// Driver program
int main()
{
    vector<int> arr = { 2, 1, 5, 3, 1, 0, 4 };
    cout << findWater(arr);
    return 0;
}

C

#include <stdio.h>

// Function to find the maximum amount of water that can be trapped
int findWater(int arr[], int n) {

    // Left[i] contains height of tallest bar to the
    // left of i'th bar including itself
    int left[n];

    // Right[i] contains height of tallest bar to
    // the right of i'th bar including itself
    int right[n];

    // Initialize result
    int res = 0;

    // Fill left array
    left[0] = arr[0];
    for (int i = 1; i < n; i++)
        left[i] = left[i - 1] > arr[i] ? left[i - 1] : arr[i];

    // Fill right array
    right[n - 1] = arr[n - 1];
    for (int i = n - 2; i >= 0; i--)
        right[i] = right[i + 1] > arr[i] ? right[i + 1] : arr[i];

    // Calculate the accumulated water element by element
    for (int i = 1; i < n - 1; i++) {
        int minOf2 = left[i - 1] < right[i + 1] ? left[i - 1] : right[i + 1];
        if (minOf2 > arr[i]) {
            res += minOf2 - arr[i];
        }
    }

    return res;
}

// Driver program
int main() {
    int arr[] = { 2, 1, 5, 3, 1, 0, 4 };
    int n = sizeof(arr) / sizeof(arr[0]);
    printf("%d", findWater(arr, n));
    return 0;
}

Java

import java.util.*;

// Function to find the maximum amount of water that can be trapped
class GfG {

    static int findWater(int[] arr) {
        int n = arr.length;

        // Left[i] contains height of tallest bar to the
        // left of i'th bar including itself
        int[] left = new int[n];

        // Right[i] contains height of tallest bar to
        // the right of i'th bar including itself
        int[] right = new int[n];

        // Initialize result
        int res = 0;

        // Fill left array
        left[0] = arr[0];
        for (int i = 1; i < n; i++)
            left[i] = Math.max(left[i - 1], arr[i]);

        // Fill right array
        right[n - 1] = arr[n - 1];
        for (int i = n - 2; i >= 0; i--)
            right[i] = Math.max(right[i + 1], arr[i]);

        // Calculate the accumulated water element by element
        for (int i = 1; i < n - 1; i++) {
            int minOf2 = Math.min(left[i - 1], right[i + 1]);
            if (minOf2 > arr[i]) {
                res += minOf2 - arr[i];
            }
        }

        return res;
    }

    // Driver program
    public static void main(String[] args) {
        int[] arr = { 2, 1, 5, 3, 1, 0, 4 };
        System.out.println(findWater(arr));
    }
}

Python

# Function to find the maximum amount of water that can be trapped
def findWater(arr):
    n = len(arr)

    # Left[i] contains height of tallest bar to the
    # left of i'th bar including itself
    left = [0] * n

    # Right[i] contains height of tallest bar to
    # the right of i'th bar including itself
    right = [0] * n

    # Initialize result
    res = 0

    # Fill left array
    left[0] = arr[0]
    for i in range(1, n):
        left[i] = max(left[i - 1], arr[i])

    # Fill right array
    right[n - 1] = arr[n - 1]
    for i in range(n - 2, -1, -1):
        right[i] = max(right[i + 1], arr[i])

    # Calculate the accumulated water element by element
    for i in range(1, n - 1):
        minOf2 = min(left[i - 1], right[i + 1])
        if minOf2 > arr[i]:
            res += minOf2 - arr[i]

    return res

# Driver program
arr = [2, 1, 5, 3, 1, 0, 4]
print(findWater(arr))

C#

using System;

class GfG {

    // Function to find the maximum amount of water that can be trapped
    static int findWater(int[] arr) {
        int n = arr.Length;

        // Left[i] contains height of tallest bar to the
        // left of i'th bar including itself
        int[] left = new int[n];

        // Right[i] contains height of tallest bar to
        // the right of i'th bar including itself
        int[] right = new int[n];

        // Initialize result
        int res = 0;

        // Fill left array
        left[0] = arr[0];
        for (int i = 1; i < n; i++)
            left[i] = Math.Max(left[i - 1], arr[i]);

        // Fill right array
        right[n - 1] = arr[n - 1];
        for (int i = n - 2; i >= 0; i--)
            right[i] = Math.Max(right[i + 1], arr[i]);

        // Calculate the accumulated water element by element
        for (int i = 1; i < n - 1; i++) {
            int minOf2 = Math.Min(left[i - 1], right[i + 1]);
            if (minOf2 > arr[i]) {
                res += minOf2 - arr[i];
            }
        }

        return res;
    }

    // Driver program
    static void Main() {
        int[] arr = { 2, 1, 5, 3, 1, 0, 4 };
        Console.WriteLine(findWater(arr));
    }
}

JavaScript

// Function to find the maximum amount of water that can be trapped
function findWater(arr) {
    let n = arr.length;

    // Left[i] contains height of tallest bar to the
    // left of i'th bar including itself
    let left = new Array(n);

    // Right[i] contains height of tallest bar to
    // the right of i'th bar including itself
    let right = new Array(n);

    // Initialize result
    let res = 0;

    // Fill left array
    left[0] = arr[0];
    for (let i = 1; i < n; i++)
        left[i] = Math.max(left[i - 1], arr[i]);

    // Fill right array
    right[n - 1] = arr[n - 1];
    for (let i = n - 2; i >= 0; i--)
        right[i] = Math.max(right[i + 1], arr[i]);

    // Calculate the accumulated water element by element
    for (let i = 1; i < n - 1; i++) {
        let minOf2 = Math.min(left[i - 1], right[i + 1]);
        if (minOf2 > arr[i]) {
            res += minOf2 - arr[i];
        }
    }

    return res;
}

// Driver program
let arr = [2, 1, 5, 3, 1, 0, 4];
console.log(findWater(arr));

Illustration

Consider arr[] = {3, 0, 2, 0, 4}


Therefore, left[] = {3, 3, 3, 3, 4} and right[] = {4, 4, 4, 4, 4}
Now consider iterating using i from 0 to end and compute water stored at every index as min(left[i], right[i]) – arr[i]) and if it is greater than 0, then add it to the result.


Initialize : res = 0
For i = 0:  res = 0  + 0 = 0
For i = 1:  res = 0 + 3 = 3
For i = 2:  res = 3 + 1 = 4
For i = 3:  res = 4 + 3 = 7
For i = 4:  res = 7 + 0 = 7


So total rain water trapped = 7