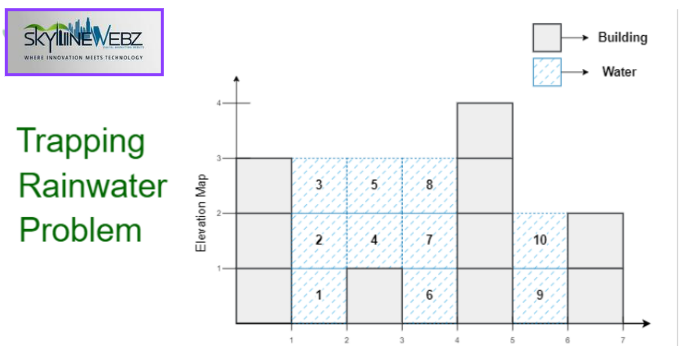
Although we have already covered a better strategy than this, this is a quite fascinating one to understand. Before advancing, it is highly advised to refer next greater element, past greater element and greatest area in a histogram difficulties. We remove an item from the stack and designate present item as next greater of it when we find next greater element. One significant finding here is the item below every item in the stack—the preceding greater element.
We can thus determine both previous greater and next greater in one traversal and a stack for every element. Now you could be asking that for the trapping rain water issue, we require best on right and left (not closest greater). Kindly stop reading for a while and consider how we might find the water using next greater and previous greater.
Using a stack and single traversal, one seeks next greater and previous greater for every element as mentioned above.
We know absolutely that we must fill water between legitimate next greater and previous greater when we have both. We fill the known amount knowing a minimal amount as well.
And when we contemplate past greater and next greater we locate their next and previous greater, and fill some more volume. We keep doing this till we discover both past and future greatest.
We fill all between next greater and previous greater; we do not exactly fill one by one and neither do we fill the exact amount in a go.
C++
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
// Function to return the maximum water that can be stored
int maxWater(vector<int>& arr) {
stack<int> st;
int res = 0;
for (int i = 0; i < arr.size(); i++) {
// Pop all items smaller than arr[i]
while (!st.empty() && arr[st.top()] < arr[i]) {
int pop_height = arr[st.top()];
st.pop();
if (st.empty())
break;
// arr[i] is the next greater for the removed item
// and new stack top is the previous greater
int distance = i - st.top() - 1;
// Take the minimum of two heights (next and prev greater)
// and find the amount of water that we can fill in all
// bars between the two
int water = min(arr[st.top()], arr[i]) - pop_height;
res += distance * water;
}
st.push(i);
}
return res;
}
// Driver code
int main() {
vector<int> arr = {2, 1, 5, 3, 1, 0, 4};
cout << maxWater(arr);
return 0;
}C
#include <stdio.h>
#include <stdlib.h>
// A structure to represent a stack
struct Stack {
int *array;
int top;
int capacity;
};
// Create a stack
struct Stack* createStack(int capacity) {
struct Stack* stack = (struct Stack*)malloc(sizeof(struct Stack));
stack->capacity = capacity;
stack->top = -1;
stack->array = (int*)malloc(capacity * sizeof(int));
return stack;
}
// Stack is full when top is equal to the last index
int isFull(struct Stack* stack) {
return stack->top == stack->capacity - 1;
}
// Stack is empty when top is -1
int isEmpty(struct Stack* stack) {
return stack->top == -1;
}
// Function to add an item to stack
void push(struct Stack* stack, int item) {
if (isFull(stack))
return;
stack->array[++stack->top] = item;
}
// Function to remove an item from stack
int pop(struct Stack* stack) {
if (isEmpty(stack))
return -1;
return stack->array[stack->top--];
}
// Function to return the top from the stack without popping
int top(struct Stack* stack) {
return stack->array[stack->top];
}
// Function to return the maximum water that can be stored
int maxWater(int* arr, int n) {
struct Stack* st = createStack(n);
int res = 0;
for (int i = 0; i < n; i++) {
// Pop all items smaller than arr[i]
while (!isEmpty(st) && arr[top(st)] < arr[i]) {
int pop_height = arr[pop(st)];
if (isEmpty(st))
break;
// arr[i] is the next greater for the removed item
// and new stack top is the previous greater
int distance = i - top(st) - 1;
// Take the minimum of two heights (next and prev greater)
int water = (arr[top(st)] < arr[i]) ? arr[top(st)] : arr[i];
// Find the amount of water
water -= pop_height;
res += distance * water;
}
push(st, i);
}
free(st->array);
free(st);
return res;
}
// Driver code
int main() {
int arr[] = {2, 1, 5, 3, 1, 0, 4};
int n = sizeof(arr) / sizeof(arr[0]);
printf("%d\n", maxWater(arr, n));
return 0;
}Java
import java.util.Stack;
class GfG {
// Function to return the maximum water that can be stored
static int maxWater(int[] arr) {
Stack<Integer> st = new Stack<>();
int res = 0;
for (int i = 0; i < arr.length; i++) {
// Pop all items smaller than arr[i]
while (!st.isEmpty() && arr[st.peek()] < arr[i]) {
int pop_height = arr[st.pop()];
if (st.isEmpty())
break;
// arr[i] is the next greater for the removed item
// and new stack top is the previous greater
int distance = i - st.peek() - 1;
// Take the minimum of two heights (next and prev greater)
int water = Math.min(arr[st.peek()], arr[i]);
// Find the amount of water
water -= pop_height;
res += distance * water;
}
st.push(i);
}
return res;
}
// Driver code
public static void main(String[] args) {
int[] arr = {2, 1, 5, 3, 1, 0, 4};
System.out.println(maxWater(arr));
}
}Python
# Function to return the maximum water that can be stored
def maxWater(arr):
st = []
res = 0
for i in range(len(arr)):
# Pop all items smaller than arr[i]
while st and arr[st[-1]] < arr[i]:
pop_height = arr[st.pop()]
if not st:
break
# arr[i] is the next greater for the removed item
# and new stack top is the previous greater
distance = i - st[-1] - 1
# Take the minimum of two heights (next and prev greater)
water = min(arr[st[-1]], arr[i])
# Find the amount of water
water -= pop_height
res += distance * water
st.append(i)
return res
# Driver code
arr = [2, 1, 5, 3, 1, 0, 4]
print(maxWater(arr))Output
9
