Trapping Rain Water Problem – Using Two Pointers

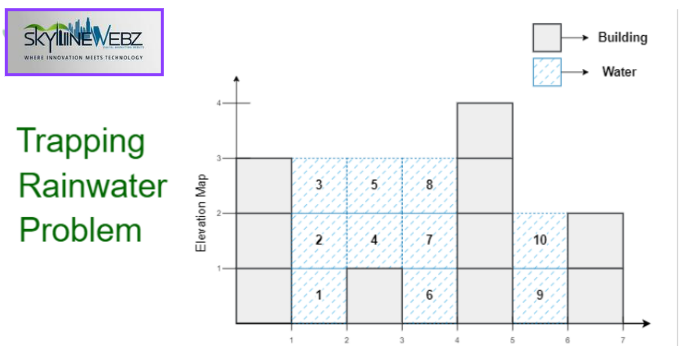
Optimal Method: Two Pointers O(n) Time and O(1) Space:

The strategy is mostly predicated on the following facts:

• Knowing the left max (max element in arr[0…left-1]) and right max (max element in arr[right+1…n-1], allows us to determine the amount of water either for arr[left] or arr[right].
• Should left max be less than the right max, we can choose arr[left]. Alternatively, we can choose arr[right].
• Should we choose arr[left], the remaining water would be left most minimally.

How can this be accomplished?

Let us examine the situation whereby left max is less than right max. We already have a bigger value in arr[right…n-1 so we know left max for arr[left] and the right max for it would not be less than left max.

C++

#include <iostream>
#include <vector>
using namespace std;

int maxWater(vector<int> &arr) { 
  
    int left = 1;
    int right = arr.size() - 2;

    // lMax : Maximum in subarray arr[0..left-1]
    // rMax : Maximum in subarray arr[right+1..n-1]
    int lMax = arr[left - 1];
    int rMax = arr[right + 1];

    int res = 0;
    while (left <= right) {
      
        // If rMax is smaller, then we can decide the amount of water for arr[right]
        if (rMax <= lMax) {
          
            // Add the water for arr[right]
            res += max(0, rMax - arr[right]);

            // Update right max
            rMax = max(rMax, arr[right]);

            // Update right pointer as we have decided the amount of water for this
            right -= 1;
        } else { 
            // Add the water for arr[left]
            res += max(0, lMax - arr[left]);

            // Update left max
            lMax = max(lMax, arr[left]);

            // Update left pointer as we have decided water for this
            left += 1;
        }
    }
    return res;
}

// Driver code
int main() {
    vector<int> arr = {2, 1, 5, 3, 1, 0, 4};
    cout << maxWater(arr) << endl;
    return 0;
}

C

#include <stdio.h>

// Function to find the maximum amount of water that can be trapped
int maxWater(int arr[], int n) {
    int left = 1;
    int right = n - 2;

    // lMax : Maximum in subarray arr[0..left-1]
    // rMax : Maximum in subarray arr[right+1..n-1]
    int lMax = arr[left - 1];
    int rMax = arr[right + 1];

    int res = 0;
    while (left <= right) {
      
        // If rMax is smaller, then we can decide the amount of water for arr[right]
        if (rMax <= lMax) {
          
            // Add the water for arr[right]
            res += (rMax - arr[right]) > 0 ? (rMax - arr[right]) : 0;

            // Update right max
            rMax = rMax > arr[right] ? rMax : arr[right];

            // Update right pointer as we have decided the amount of water for this
            right -= 1;
        } else { 
            // Add the water for arr[left]
            res += (lMax - arr[left]) > 0 ? (lMax - arr[left]) : 0;

            // Update left max
            lMax = lMax > arr[left] ? lMax : arr[left];

            // Update left pointer as we have decided water for this
            left += 1;
        }
    }
    return res;
}

// Driver code
int main() {
    int arr[] = {2, 1, 5, 3, 1, 0, 4};
    int n = sizeof(arr) / sizeof(arr[0]);
    printf("%d\n", maxWater(arr, n));
    return 0;
}

Java

import java.util.*;

class GfG {

    // Function to find the maximum amount of water that can be trapped
    static int maxWater(int[] arr) {
        int left = 1;
        int right = arr.length - 2;

        // lMax : Maximum in subarray arr[0..left-1]
        // rMax : Maximum in subarray arr[right+1..n-1]
        int lMax = arr[left - 1];
        int rMax = arr[right + 1];

        int res = 0;
        while (left <= right) {
          
            // If rMax is smaller, then we can decide the amount of water for arr[right]
            if (rMax <= lMax) {
              
                // Add the water for arr[right]
                res += Math.max(0, rMax - arr[right]);

                // Update right max
                rMax = Math.max(rMax, arr[right]);

                // Update right pointer as we have decided the amount of water for this
                right -= 1;
            } else { 
              
                // Add the water for arr[left]
                res += Math.max(0, lMax - arr[left]);

                // Update left max
                lMax = Math.max(lMax, arr[left]);

                // Update left pointer as we have decided water for this
                left += 1;
            }
        }
        return res;
    }

    // Driver code
    public static void main(String[] args) {
        int[] arr = {2, 1, 5, 3, 1, 0, 4};
        System.out.println(maxWater(arr));
    }
}

Python

# Function to find the maximum amount of water that can be trapped
def maxWater(arr):
    left = 1
    right = len(arr) - 2

    # lMax : Maximum in subarray arr[0..left-1]
    # rMax : Maximum in subarray arr[right+1..n-1]
    lMax = arr[left - 1]
    rMax = arr[right + 1]

    res = 0
    while left <= right:
      
        # If rMax is smaller, then we can decide the amount of water for arr[right]
        if rMax <= lMax:
          
            # Add the water for arr[right]
            res += max(0, rMax - arr[right])

            # Update right max
            rMax = max(rMax, arr[right])

            # Update right pointer as we have decided the amount of water for this
            right -= 1
        else: 
          
            # Add the water for arr[left]
            res += max(0, lMax - arr[left])

            # Update left max
            lMax = max(lMax, arr[left])

            # Update left pointer as we have decided water for this
            left += 1
    return res

if __name__ == "__main__":
    arr = [2, 1, 5, 3, 1, 0, 4]
    print(maxWater(arr))

C#

using System;

class GfG {

    // Function to find the maximum amount of water that can be trapped
    static int maxWater(int[] arr) {
        int left = 1;
        int right = arr.Length - 2;

        // lMax : Maximum in subarray arr[0..left-1]
        // rMax : Maximum in subarray arr[right+1..n-1]
        int lMax = arr[left - 1];
        int rMax = arr[right + 1];

        int res = 0;
        while (left <= right) {
          
            // If rMax is smaller, then we can decide the amount of water for arr[right]
            if (rMax <= lMax) {
              
                // Add the water for arr[right]
                res += Math.Max(0, rMax - arr[right]);

                // Update right max
                rMax = Math.Max(rMax, arr[right]);

                // Update right pointer as we have decided the amount of water for this
                right -= 1;
            } else { 
                // Add the water for arr[left]
                res += Math.Max(0, lMax - arr[left]);

                // Update left max
                lMax = Math.Max(lMax, arr[left]);

                // Update left pointer as we have decided water for this
                left += 1;
            }
        }
        return res;
    }

    // Driver code
    static void Main() {
        int[] arr = {2, 1, 5, 3, 1, 0, 4};
        Console.WriteLine(maxWater(arr));
    }
}

JavaScript

// Function to find the maximum amount of water that can be trapped
function maxWater(arr) {
    let left = 1;
    let right = arr.length - 2;

    // lMax : Maximum in subarray arr[0..left-1]
    // rMax : Maximum in subarray arr[right+1..n-1]
    let lMax = arr[left - 1];
    let rMax = arr[right + 1];

    let res = 0;
    while (left <= right) {
      
        // If rMax is smaller, then we can decide the amount of water for arr[right]
        if (rMax <= lMax) {
          
            // Add the water for arr[right]
            res += Math.max(0, rMax - arr[right]);

            // Update right max
            rMax = Math.max(rMax, arr[right]);

            // Update right pointer as we have decided the amount of water for this
            right -= 1;
        } else { 
            // Add the water for arr[left]
            res += Math.max(0, lMax - arr[left]);

            // Update left max
            lMax = Math.max(lMax, arr[left]);

            // Update left pointer as we have decided water for this
            left += 1;
        }
    }
    return res;
}

// Driver code
let arr = [2, 1, 5, 3, 1, 0, 4];
console.log(maxWater(arr));